Beugung am Doppelspalt
| Beugung am Doppelspalt | |
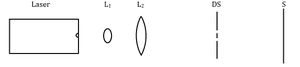
 Aufbau zur Beugung am Doppelspalt | |
| Kurzbeschreibung | |
|---|---|
| Mit dem Experiment Beugung am Doppelspalt soll eine Messung der Wellenlänge des Lasers unter Beachtung der Messfehler erfolgen. | |
| Kategorien | |
| Optik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | System, Wechselwirkung, Energie oder Materie |
| Sonstiges | |
| Durchführungsform | Schüler*innen-Experiment, Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Anna Elisabeth Heine |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Stephan Pfeiler |
Schon 1678 wurde von Christiaan Huygens eine erste Theorie darüber vorgelegt, dass Licht Welleneigenschaften besitzt (vgl. Halliday [1] (2007), S.744). Jedoch wurde erst 1807 von Thomas Young ein Experiment vorgestellt, welches die Bestätigung der Wellentheorie lieferte (vgl. Kuhn [2] (1992), S.85). Das Doppelspalt-Experiment dient noch heute, als einfache Möglichkeit diese Eigenschaft des Lichtes darzustellen.
Inhaltsverzeichnis
Didaktischer Teil
Bis ins 19. Jahrhundert wurden Experimente zur Gewinnung von neuen Theorien durchgeführt, ohne die Messunsicherheiten zu beachten. Heute nehmen sie beim Experimentieren in der Forschung eine wichtige Rolle ein. Dies gilt jedoch nicht für die Schule. Hier werden die Messunsicherheiten in den überwiegenden Fällen nicht betrachtet und wenn doch, dann nur im Anschluss mit der Frage "Welche Fehlerquellen können auftreten und wie können diese verhindert werden?".
In den Bildungsstandards der KMK im Fach Physik für den mittleren Schulabschluss sind zu dem Thema "Messunsicherheiten, Messfehler, Messabweichung" keinerlei Hinweise zu finden (vgl. KMK [3] (2005)). Im Berliner Rahmenlehrplan für die Sekundarstufe I in Physik ist lediglich im Thema P6 der Jahrgangsstufe 7/8 Körper bewegen: Mechanik die Könnenserwartung festgehalten, dass die Schülerinnen und Schüler "bei Messreihen [...] einfache Fehlerbetrachtungen [durchführen] und bei der Auswertung [berücksichtigen sollen] [...]" (vgl. Senatsverwaltung für Bildung, Jugend und Sport [4] (2006), S. 30). Nur im Wahlpflichtfach wird den Messunsicherheiten im Thema WP10 Größen messen und Messfehler betrachten Aufmerksamkeit geschenkt. Im Lehrplan der Sekundarstufe II steht dann unter der Kompetenz Erkenntnisgewinnung, dass die Schülerinnen und Schüler in der Lage sein müssen, Ergebnisse mithilfe von Fehlerbetrachtungen zu dokumentieren. Dies soll möglichst unter der Anwendung des eigenen Wissens über experimentelles Arbeiten geschehen (vgl. Senatsverwaltung für Bildung, Jugend und Sport [5] (2006)). Problematisch erscheint, wie die Schülerinnen und Schüler ohne Vorwissen Fehlerbetrachtungen durchführen können.
Julia Hellwig hat im Rahmen ihrer Dissertation das reduzierte Sachstrukturmodell entwickelt, welches die Behandlung von Messunsicherheiten im Schulunterricht vereinfachen und vereinheitlichen soll. Dabei nimmt sie eine Kategorisierung von Teilaspekten zur Messunsicherheit vor. Das Sachstrukturmodell ist untergliedert in 4 Dimensionen:
- Grundsätzliche Existenz von Messunsicherheiten
- Einfluss von Messunsicherheiten auf das Messwesen
- Erfassung von Messunsicherheiten
- Aussagekraft von Messunsicherheiten
Unter dem Punkt Grundsätzliche Existenz von Messunsicherheiten soll unter anderem eine Unterscheidung von Messabweichung und Messunsicherheit erfolgen und die Ursachen von Messunsicherheiten besprochen werden. "In der zweiten Dimension wird darauf eingegangen, inwiefern Messunsicherheiten mit dem Messprozess verbundene Sichtweisen und daraus resultierende Entscheidungen beeinflussen, die bei der Planung und Durchführung einer Messung zu treffen sind" (Hellwig [6] (2012), S. 63). Im nächsten Schritt geht es um die Erfassung von Messunsicherheiten. Hier unterscheidet Hellwig zwischen einer direkten (Erfassung einer Unsicherheitskomponente) und einer indirekten (Fehlerfortpflanzung) Messung. Bei der Aussagekraft von Messunsicherheiten gilt es die Messwerte zu vergleichen und zu Diskutieren inwiefern die Messung und ihre Ergebnisse verlässlich sind. (vgl. Hellwig [6] (2012), S. 61-82)
Versuchsanleitung
Der Versuch wurde zum Teil unter Verwendung der Anleitung nach Leybold aufgebaut und durchgeführt (siehe [5] Leybold).
Aufbau
Geräte
| 1 | Optische Bank | |
| 5 | Optikreiter | |
| 1 | He-Ne-Laser, linear polarisiert | |
| 1 | Linse f=+5mm | |
| 1 | Linse f=+50mm | |
| 1 | Halter mit Federklemme | |
| 1 | Blende mit 3 Doppelspalten | |
| 1 | Schirm | |
| 1 | Blatt Papier | |
| 1 | Lineal |
Beschreibung
Die fünf Optikreiter sind für den Laser, die Linsen, den Halter und den Schirm vorgesehen. Diese werden, wie in Abbildung 1 zusehen, nacheinander auf der optischen Bank aufgebaut. An dem Schirm wird ein weißes Blatt befestigt, damit die Abstände der Maxima aufgezeichnet werden können.
Für die Justierung des Lasers sind folgende Schritte einzuhalten:
- Zunächst wird der He-Ne-Laser auf der Optischen Bank befestigt. Im Anschluss wird in einem Abstand von etwa 190cm der Schirm aufgestellt. (Sollte keine 2m lange Optische Bank zur Verfügung stehen, kann der Schirm mit einem Sockel auf einem weiteren Tisch gestellt werden.)
- Nun wird der Laser auf den Schirm gerichtet und eingeschalten.
- Der Halter mit den Doppelspalten wird in einem Abstand von ca. 50 cm vom Laser aufgestellt. Dabei wird der Laser so ausgerichtet, dass der Laserstrahl in der Höhe durch die Mitte des Doppelspalts verläuft.
- Nun wird in einem Abstand von 1 cm die Linse L1 mit der Brennweite f=+5mm vor den Laser platziert. Dabei sollte der Laser die Blende gut ausleuchten. Anschließend wird der Halter wieder entfernt.
- Die Linse L2 mit der Brennweite f=+50mm wird mit einem Abstand von ca. 55 mm hinter der Linse L1 platziert.
- Nun wird der Halter mit den Doppelspalten wieder auf der Optischen Bank befestigt.
Der Versuch kann auch ohne Linsen durchgeführt werden (siehe Abbildung 2).
Durchführung
Der Versuch wird im Folgenden einmal ohne Linsen durchgeführt und einmal mit. Der Laser wird wie im Aufbau beschrieben auf den Doppelspalt, beginnend bei d=0,2mm, gerichtet. Nun wird der Schirm zu beginn im Abstand von 50 cm vom Doppelspalt befestigt. Auf dem weißen Blatt werden die Maxima mit einem gespitzten Bleistift kenntlich gemacht. Markiert werden sollten die Maxima 0. und 1. Ordnung (x1), wenn es die Lichtverhältnisse zulassen und die Intensität hoch genug ist, können auch weitere Ordnungen aufgenommen werden. Hierbei ist darauf zu achten, so gut wie möglich die Mitte der Maxima zu nehmen. Danach wird der Abstand vom Doppelspalt zum Schirm vergrößert (e=80cm, e=100cm, e=120cm und e=140cm). Im Anschluss wird der Vorgang mit einem Doppelspalt mit verschiedenen Spaltabständen (d=0,3mm und d=0,4mm) wiederholt.
Sind alle Maxima auf dem Blatt kenntlich gemacht worden. So folgt die Messung der Abstände der Maxima, hierfür kann ein Lineal verwendet werden. Die Ergebnisse werden in einer Tabelle notiert.
Ergebnisse
Die Spaltbreite d, die Entfernung Schirm-Spalt e und der Abstand der Maxima x ist stets in mm angegeben.
| d=0,2 | d=0,3 | d=0,4 | |
|---|---|---|---|
| e=500 | 1,9 | 1 | 1 |
| e=800 | 2,5 | 1,5 | 1,5 |
| e=1000 | 3 | 2 | 1,5 |
| e=1200 | 4 | 2,5 | 2 |
| e=1400 | 4 | 3 | 2,5 |
| d=0,2 | d=0,3 | d=0,4 | |
|---|---|---|---|
| e=500 | 3 | 2 | 1,5 |
| e=800 | 5 | 3,5 | 2,5 |
| e=1000 | 6 | 4 | 3 |
| e=1200 | 8 | 5 | 4 |
| e=1400 | 8 | 6 | 5 |
| d=0,2 | d=0,3 | d=0,4 | |
|---|---|---|---|
| e=500 | 1 | 1 | 0,8 |
| e=800 | 2,1 | 1,2 | 1 |
| e=1000 | 3 | 2 | 1,2 |
| e=1200 | 3,5 | 2,1 | 1,5 |
| e=1400 | 3 | 1,8 |
Auswertung
Die in der folgenden Tabelle angegebenen theoretischen Werte dienen als Vergleichswerte.
| x1 | x2 | |||||
|---|---|---|---|---|---|---|
| d=0,2 | d=0,3 | d=0,4 | d=0,2 | d=0,3 | d=0,4 | |
| e=500 | 1,6 | 1,1 | 0,8 | 3,2 | 2,1 | 1,6 |
| e=800 | 2,5 | 1,7 | 1,3 | 5,1 | 3,4 | 2,5 |
| e=1000 | 3,2 | 2,1 | 1,6 | 6,3 | 4,2 | 3,2 |
| e=1200 | 3,8 | 2,5 | 1,9 | 7,6 | 5,1 | 3,8 |
| e=1400 | 4,4 | 3 | 2,2 | 8,9 | 5,9 | 4,4 |
Ziel dieses Experimentes ist es, die Wellenlänge des He-Ne-Lasers zu bestimmten und mit dem gegebenen Referenzwert von 632,8 nm zu vergleichen. Dafür wird die folgende Formel benötigt:
Daraus ergeben sich die folgenden Werte:
| d=0,2 | d=0,3 | d=0,4 | |
|---|---|---|---|
| e=500 | 760,00 | 600,00 | 800,00 |
| e=800 | 625,00 | 562,50 | 750,00 |
| e=1000 | 600,00 | 600,00 | 600,00 |
| e=1200 | 666,67 | 625,00 | 666,67 |
| e=1400 | 571,43 | 642,86 | 714,29 |
| d=0,2 | d=0,3 | d=0,4 | |
|---|---|---|---|
| e=500 | 600,00 | 600,00 | 600,00 |
| e=800 | 625,00 | 656,25 | 625,00 |
| e=1000 | 600,00 | 600,00 | 600,00 |
| e=1200 | 666,67 | 625,00 | 666,67 |
| e=1400 | 571,43 | 642,86 | 714,29 |
| d=0,2 | d=0,3 | d=0,4 | |
|---|---|---|---|
| e=500 | 400,00 | 600,00 | 640,00 |
| e=800 | 525,00 | 450,00 | 500,00 |
| e=1000 | 600,00 | 600,00 | 480,00 |
| e=1200 | 583,33 | 525,00 | 500,00 |
| e=1400 | 642,86 | 514,29 |
Berechnung des Mittelwerts:
Ohne Linse:
Mit Linse:
Für die Berechnung der zufälligen Messabweichung gilt:
mit
Damit ergibt sich ein Messergebnis von:
Die Wellenlänge des genutzten Lasers beträgt .
Bei Betrachtung der Werte der Wellenlängen bei der Bestimmung mit Linsen kann festgestellt werden, dass sie bis auf zwei Werte alle unter dem angegebenen Referenzwert liegen. Daraus kann geschlossen werden, dass die Justierung der Linsen nicht exakt durchgeführt wurde und somit eine systematische Messabweichung berücksichtigt werden müsste. Eine solche Korrekturrechnung kann in der Schule jedoch nicht durchgeführt werden und wird an dieser Stelle nicht betrachtet. Die Ergebnisse können genutzt werden, um mit den Schülerinnen und Schülern über systematische Messabweichungen zu reden. Im Anschluss kann eine Korrektur des Aufbaus vorgenommen und erneut eine Messreihe aufgenommen werden.
Sicherheitshinweise
- Nicht in den direkten oder reflektierten Laserstrahl blicken
- Überschreitung der Blendungsgrenze vermeiden (d.h. kein Beobachter darf direkt geblendet werden!)
Literatur
- ↑ Halliday,D., Resnick, R., Walker, J. (2007): Halliday Physik. Bachelor Edition; WILEY-VCH Verlag GmbH & Co. KGaA Weinheim
- ↑ Kuhn, W. (1992): Handbuch deer experimentellen Physik. Sekundarbereich II. Band 4/I: Optik; Aulis Verlag Deubner & Co KG Köln
- ↑ Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland (Hrsg.) (2005): Bildungsstandards im Fach Physik für den Mittleren Schulabschluss; München, Neuwied. Verfügbar unter [1][06.09.2016]
- ↑ Senatsverwaltung für Bildung, Jugend und Sport (Hrsg.) (2006): Rahmenlehrplan für die Sekundarstufe I. Jahrgangsstufe 7-10. Hauptschule, Realschule, Gesamtschule, Gymnasium. Physik; Berlin. Verfügbar unter [2][06.09.2016]
- ↑ Senatsverwaltung für Bildung, Jugend und Sport (Hrsg.) (2006): Rahmenlehrplan für die gymnasiale Oberstufe. Gymnasien, Gesamtschulen mit gymnasialer Oberstufe, Berufliche Gymnasien, Kollegs, Abendgymnasien. Physik; Berlin. Verfügbar unter [3][06.09.2016]
- ↑ 6,0 6,1 Hellwig, J. (2012): Messunsicherheiten verstehen. Entwicklung eines normativen Sachstrukturmodells am Beispiel des Unterrichtsfaches Physik; Bochum. Verfügbar unter [4] [05.09.2016] Referenzfehler: Ungültiges
<ref>-Tag. Der Name „Hellwig“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert.
Siehe auch
- Hellwig, J. (2012): Messunsicherheiten verstehen; http://www-brs.ub.ruhr-uni-bochum.de/netahtml/HSS/Diss/HellwigJulia/diss.pdf [05.09.2016]
- LYBOLD: Beugung am Doppelspalt und an Mehrfachspalten; http://www.ld-didactic.de/documents/de-DE/EXP/P/P5/P5312_d.pdf?_ga=1.248338759.173817620.1473084785 [05.09.2016]