Bestimmung des Induktionsgesetzes bei konstanter durchsetzter Fläche
| Bestimmung des Induktionsgesetzes bei konstanter durchsetzter Fläche | |
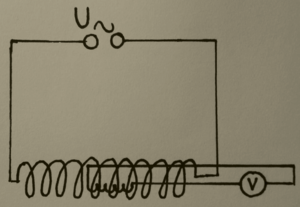
 Experimentaufbau mit noch nicht eingeführter Induktionsspule | |
| Kurzbeschreibung | |
|---|---|
| Bei diesem Experiment soll das Induktionsgesetz bei konstanter Fläche überprüft werden. Schülerinnen und Schüler sollen ein Verständnis für das Zusammenspiel der Größen, die einen Einfluss haben. | |
| Kategorien | |
| Elektrizitätslehre, Induktion | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment mit Schülerbeteiligung |
| Anzahl Experimente in dieser Unterkategorie | 3 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Franziska Vaihinger |
| Kontakt: | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\text{vaihinger}}} @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Wiebke Musold |
Ab der Wende zum 20. Jahrhundert breitete sich die flächendeckende Stromversorgung aus (siehe [2] Westdeutscher Rundfunk Köln). Damals wie heute ist man bemüht diese Versorgung zu optimieren. Im Jahre 2015 sind verschiedene Arten von Kraftwerken in Betrieb, die elektrischen Strom in das genutzte Stromnetz speisen. Ein grundlegendes Prinzip, welches vielen dieser Kraftwerke zu Grunde liegt, ist die Induktion. Das hier beschriebene Experiment dient der Überprüfung des Induktionsgesetzes bei konstanter durchsetzter Fläche.
Inhaltsverzeichnis
Didaktischer Teil
Das beschriebene Experiment dient der quantitativen Überprüfung eines physikalischen Gesetzes und der Verständnisförderung für einen physikalischen Zusammenhang. Dieses soll durch eine bestimmte Variation einzelner Einflussgrößen und deren Auswirkungen auf die Induktionsspannung geschehen. In der Versuchsanleitung wird hierfür eine konkrete Abfolge einzelner Schritte beschrieben. Diese kann analog mit Schülerinnen und Schülern durchgeführt werden.
Das Experiment als Medium kann das Verständnis von Schülerinnen und Schülern für Zusammenhänge von physikalischen Größen fördern. Dieses Ziel gehört der Klasse der Konzeptzielen an. Das sind kognitive Ziele, die den Schülerinnen und Schülern neben Wissen und Fakten auch Begriffe, Theorien und Zusammenhänge näher bringen. In der hier beschriebenen Versuchsreihe werden in drei Versuchsteilen jeweils ein Teilaspekt der kompletten Formel betrachtet. Die übrigen werden dabei konstant gehalten. So wird die Aufmerksamkeit der Schülerinnen und Schüler auf eine Teilabhängigkeit gelenkt. Dadurch entsteht die Möglichkeit diese als einzelnes zu begreifen und zu verstehen. Indessen wird jedes Mal in zwei Größen unterschieden: zum einen die wichtige Einflussgröße, welche die zu untersuchende Größe ist, und zum anderen den unwesentlichen Einflussgrößen, die in anderen Versuchsteilen betrachtet werden. Dabei kann der erste Versuchsteil stark vorgegeben und gemeinsam die erste Einflussgröße untersucht werden. Dieses soll als Beispiel für die zwei folgenden Versuchsteile dienen. Im zweiten und dritten Versuchsteil können die Schülerinnen und Schüler analog vorgehen und so das bewusste Untersuchen verschiedener Einflussgrößen trainieren. Durch dieses Training wird das Wissen über experimentelles Arbeiten (Planung, Durchführung, Dokumentation, Auswertung, Fehlerbetrachtung) gefestigt und angewendet. Diese Kompetenz wird vom Rahmenlehrplan für die gymnasiale Oberstufe für Physik von der Senatsverwaltung für Bildung, Jugend und Sport Berlin angeführt (vgl. Senatsverwaltung für Bildung, Jugend und Sport Berlin [1] (2006), S.15). Anschließend wird das erlangte Wissen in Beziehung gesetzt, um eine Formel zu überprüfen. Dazu müssen auf einer abstrakteren Ebene Denkprozesse geleistet werden, welche Größen in Formelzeichen übertragen und Formelzeichen in mathematischen Zusammenhänge bringen. Es muss betont werden, dass die Untersuchung eines physikalischen Gesetzes einer Unterscheidung zwischen wichtiger und unwesentlichen Einflussgrößen ein hohes Maß an physikalischem Verständnis bedarf. Zudem ist das Erkennen der funktionellen Zusammenhänge und das Übersetzen dieser in eine physikalische und mathematische Ausdrucksweise eine wesentliche kognitive Kompetenz, die Schülerinnen und Schüler im Physikunterricht erlernen und einüben sollen (vgl.Kirchner,Girwidz und Häußler [2] (2001), S.285). Durch geeignete Anleitung und Einbettung in die Unterrichtsreihe stellt dieses Experiment eine Übung dafür dar.
Versuchsanleitung
Aufbau
Benötigt werden:
- Netzteil
- Verbindungskabel
- große felderzeugende Spule
- Set kleiner Induktionsspulen (je min. 2 mit verschiedener Wicklungen und Querschnitten)
- Multimeter
- Stativ
Das Netzteil und die felderzeugende Spule müssen verbunden werden. Damit die Induktionsspule bei Veränderungen der Variablen an die selbe Stelle platziert werden kann ist das Stativ mit einer Markierung zu versehen, was den systematischen Fehler verringert. An der jeweilig genutzten Induktionsspule ist ein Multimeter anzuschließen.
Durchführung
Der Versuch wird in drei Teilversuchen durchgeführt. In jedem Teilversuch wird eine Variable bewusst variiert und die übrigen konstant gehalten.
1. Betrachtung der Abhängigkeit von induzierter Spannung und Anzahl an Wicklungen
Für diesen Teil des Versuches wird die Induktionsspule aus dem Set benötigt, bei der durch Auswahl zweier Buchsen verschiedene Windungen bei gleichem Querschnitt abgegriffen werden können. Diese wird mit Hilfe des Stativs in die felderzeugende Spule geführt. Das Netzteil wird auf 10 A Wechselstrom eingestellt und das Multimeter angeschaltet. Es werden sechs Messungen für alle möglichen Windungszahlen durchgeführt.
2. Betrachtung der Abhängigkeit von induzierter Spannung und der Querschnittfläche der Induktionsspule
Nun wird die Spule ausgetauscht, so dass eine Induktionsspule mit einer gleichen Anzahl an Windungen, jedoch einer anderen Querschnittfläche, genutzt wird. Die Markierung an dem Stativ ermöglicht eine gleiche Tiefe bei der Einführung. Das Netzteil wird auf 10 A Wechselstrom eingestellt und das Multimeter angeschaltet. Ebenfalls werden durch Wiederholung der Schritte 6 Werte ermittelt.
3. Betrachtung der Abhängigkeit von induzierter Spannung und des sich ändernden Magnetfeldes
Nachdem Variablen bei der Induktionsspule verändert wurden folgt an dieser Stelle eine Änderung bei der felderzeugenden Spule.
Mit der Annahme, dass die Frequenz des sinusförmigen Stroms bei verschiedenen Stromstärken gleich ist, gilt, dass die Änderung des Magnetfeldes bei größerem Wechselstrom, mit konstanter Anzahl der Windungen und Länge der felderzeugenden Spule, ebenfalls größer ist. Der Grund ist, dass der Faktor Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \mu _{0}{\frac {N}{l}}} für verschiedene gleich ist und so nur die Stromstärke auf das Magnetfeld Einfluss hat. Wird der Scheitelwert der sinusförmigen Stromstärke vergrößert, so vergrößert sich auch die maximale Änderung der Stromstärke und demnach als zeitliche Änderung der Stromstärke, da aus der oben getroffenen Annahme folgt, dass für verschiedene Scheitelwerte der Stromstäre gleich groß ist. So hängt die zeitliche Änderung des Magnetfeldes Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\frac {\Delta B}{\Delta t}}=\mu _{0}{\frac {N}{l}}{\frac {\Delta I}{\Delta t}}} lediglich von dem Scheitelwert der Stromstärke ab.
Nach diesen Vorüberlegungen kann nun das Netzteil auf 5 A Wechselstrom eingestellt und das Multimeter angeschaltet werden. Um die aufgenommenen Messwerte vergleichen zu können werden auch hier ebenfalls sechs Werte aufgenommen. Diese können in der
Auswertung mit jenen aus Teil zwei verglichen werden.
Ergebnisse
Die folgenden Messergebnisse sind, wie in der Versuchsanleitung beschrieben, aufgenommen worden und tabellarisch dargestellt. Die angegebenen Fehler wurden wie folgt berechnet: Für das Multimeter wurde ein Fehler von 1% des Messwertes zuzüglich 3 Digit benutzt. Auf Grund von einem fehlerbehafteten Netzteil und anderen Bauteilen, wurden die Fehler aufgerundet. Aus Versuchsteil 1, Betrachtung der Abhängigkeit von induzierter Spannung und Anzahl an Wicklungen:
| Mittelwert | ||||||||
|---|---|---|---|---|---|---|---|---|
| N=100 | Uind [±0,007 V] | 0,309 | 0,310 | 0,310 | 0,308 | 0,306 | 0,306 | 0,308 |
| N=200 | Uind [±0,01 V] | 0,608 | 0,608 | 0,607 | 0,610 | 0,609 | 0,609 | 0,609 |
| N=300 | Uind [±0,02 V] | 0,913 | 0,910 | 0,911 | 0,910 | 0,910 | 0,911 | 0,911 |
Tabelle 1: Induktionsspannung in Abhängigkeit der Windungszahl der Induktionsspule bei konstanter Magnetfeldänderung und durchsetzter Querschnittfläche
Aus Versuchsteil 2, Betrachtung der Abhängigkeit von induzierter Spannung und der Querschnittfläche der Induktionsspule:
| Mittelwert | ||||||||
|---|---|---|---|---|---|---|---|---|
| A=25cm2 | Uind [±0,02 V] | 0,932 | 0,933 | 0,929 | 0,929 | 0,926 | 0,928 | 0,930 |
| A=10cm2 | Uind [±0,007 V] | 0,381 | 0,377 | 0,377 | 0,376 | 0,374 | 0,375 | 0,377 |
Tabelle 2: Induktionsspannung in Abhängigkeit der durchsetzten Querschnittfläche bei konstanter Magnetfeldänderung und Windungszahl der Induktionsspule
Aus Versuchsteil 3, Betrachtung der Abhängigkeit von induzierter Spannung und des sich ändernden Magnetfeldes: Der Ablesefehler wurde für das Netzgerät auf einen halben Skalenanteil abgeschätzt (0,25 A). Die Länge der felderzeugenden Spule betrug 0,6 m. Das maximale Magnetfeld wurde mittels der Formel 1 berechnet. Der zugehörige Fehler berechnet sich mittels Gauß'scher Fehlerfortpflanzung über die Formel:
- Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle u_{B}={\sqrt {({\frac {\partial B}{\partial I}}\cdot u_{I})^{2}}}}
mit
- Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\frac {\partial B}{\partial I}}=\mu _{0}{\frac {N}{l}}}
| Mittelwert | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| I=10A | (6,3±0,1)10-3 | Uind [±0,007 V] | 0,380 | 0,380 | 0,379 | 0,377 | 0,375 | 0,374 | 0,378 |
| I=5A | (3,1±0,1)10-3 | Uind [±0,005 V] | 0,180 | 0,180 | 0,180 | 0,181 | 0,182 | 0,181 | 0,181 |
Tabelle 3: Induktionsspannung in Abhängigkeit der Magnetfeldänderung der felderzeugenden Spule bei konstanter Windungszahl und durchsetzter Querschnittfläche der Induktionsspule
Auswertung
Mit den in den Ergebnissen angegeben Werten lässt sich erkennen, dass im Versuchsteil 1 bei einer größeren Anzahl an Wicklungen eine größere induzierte Spannung gemessen wurde. In den anderen Versuchsteilen verhält es sich ähnlich: Bei einer größeren Querschnittfläche, die von dem sich ändernden Magnetfeld durchsetzt wird, zeigt das Multimeter einen größeren Wert an. Auch bei einer größeren Stromstärke und dem damit größeren sich änderten Magnetfeld, wird eine höhere Induktionsspannung abgelesen. Festzuhalten ist, dass in allen Fällen eine Vergrößerung der Variable eine größere Induktionsspannung zur Folge hat. Interessant ist die Betrachtung, ob diesem Verhalten eine Gesetzmäßigkeit zu Grunde liegt, um gegebenenfalls Induktionsspannungen bei verschiedenen Spulen und Stromstärken vorherzusagen.
Betrachtet man die Ergebnisse genau, so lässt sich in allen drei Versuchsteilen eine Proportionalität feststellen. Dazu wurden die Verhältnisse der Variablen und der berechneten Mittelwerte für alle Versuchsteile bestimmt und tabellarisch dargestellt.
| Dezimalwert | gerundeter Wert | Dezimalwert | gerundeter Wert | Dezimalwert | gerundeter Wert | |
| Verhältnis der Windungszahlen | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\frac {200}{100}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{300}{200}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,5} | |
| Verhältnis der Mittlwerde der Induktionsspannung | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{0,609}{0,308}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,98} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{0,911}{0,308}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2,96} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{0,911}{0,609}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,50} |
Tabelle 4: Übersicht der Verhältnisse von Windungszahlen und Mittelwerte der gemessenen Induktionsspannung in Versuchsteil 1. Verhältnisse der Mittelwerte sind auf die dritte Nachkommastelle gerundet.
| Dezimalwert | gerundeter Wert | |
| Verhältnis der Querschnittflächen | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{25}{10}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2,5} |
| Verhältnis der Mittelwerte der Induktionsspannung | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{0,930}{0,377}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2,47} |
Tabelle 5: Vergleich der Verhältnisse der vom sich änderten Magnetfeld durchsetzten Querschnittfläche und der Mittelwerte der gemessenen Induktionsspannungen aus dem zweiten Versuchsteil. Verhältnisse der Mittelwerte sind auf die dritte Nachkommastelle gerundet.
| Dezimalwert | gerundeter Wert | |
| Verhältnis der Stromstärken | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{10}{5}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2} |
| Verhältnis der maximalen Magnetfelder | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{6,3\cdot 10^{-3}}{3,1\cdot 10^{-3}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2,03} |
| Verhältnis der Mittelwerte der Induktionsspannung | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{0,378}{0,180}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2,1} |
Tabelle 6: Vergleich der Verhältnisse der Stromstärken, maximalen Magnetfelder und der Mittelwerte der Induktionsspannung aus Versuchsteil 3. Es wurde auf die dritte Nachkommastelle gerundet.
Im Vergleich stimmen die Verhältnisse in allen drei Versuchsteilen ungefähr überein. Die Ungenauigkeiten sind auf die Messungen zurückzuführen. Diese Ergebnisse ermöglichen einen proportionalen Zusammenhang aufzuzeigen. Die Induktionsspannung ist demnach proportional zur Anzahl der Wicklungen, der durchsetzten Querschnittfläche der Induktionsspule und der Stärke des sich ändernden Magnetfeldes. Diese Überlegungen führen zum Induktionsgesetz mit fester durchsetzter Querschnittfläche A.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{ind}=N\cdot A\cdot \frac{\Delta B}{\Delta t}}
Ausblick
Der Aufbau des Experiments ist so gewählt, dass die Induktionsspule immer gleich tief in der felderzeugenden Spule geführt wird. Zudem liegen die beiden Längsachsen parallel zueinander. In einem weiterführenden Experiment kann die Winkelabhängigkeit untersucht werden und die eigentliche Ursache dieser diskutiert werden (siehe [3] Wiley Information Services GmbH). Zudem ist das hier beschriebene Experiment zur Überprüfung des Induktionsgesetzes nur hinreichend geeignet, da es die Änderung des magnetischen Flusses nicht betrachtet und sich lediglich auf die Magnetfeldänderung beschränkt. Es ist demnach interessant weitere Experimente zu betrachten, die sich mit einer zeitlichen Flächenänderung bei konstantem Magnetfeld beschäftigen. Außerdem schließt sich als Zusammenführung die Betrachtung der zeitlichen Änderung des magnetischen Flusses an.
Literatur
- ↑ Senatsverwaltung für Bildung, Jugend und Sport Berlin (2006): Rahmenlehrplan für die gymnasiale Oberstufe - Physik; 1.Auflage; verfügbar unter [1] Oldenbourg [17.03.2015]
- ↑ Kirchner, E; Girwidz, R; häußler,p. (2001): Physikdidaktik - Eine Einführung; Springer Verlag, Berlin Heidelberg New York Barcelona Hongkong London Mailand Paris Tokio
Siehe auch
- Elektromagnetische Induktion
- Entdeckung der elektromagnetischen Induktion mit Hilfe der historischen Ringkernanordnung
- Westdeutscher Rundfunk Köln: Elektrizität; http://www.planet-wissen.de/natur_technik/energie/elektrizitaet/index.jsp [10.05.2012]
- Wiley Information Services GmbH: Magnetische Induktion-Induktion bei Änderung des Magnetfeldes; http://www.chemgapedia.de/vsengine/vlu/vsc/de/ph/14/ep/einfuehrung/magnetfeld/induktion.vlu/Page/vsc/de/ph/14/ep/einfuehrung/magnetfeld/induktion/induktion02.vscml.html [03.03.2015]