Bestimmung der Lichtgeschwindigkeit in verschiedenen Ausbreitungsmedien
| Bestimmung der Lichtgeschwindigkeit in verschiedenen Ausbreitungsmedien | |
 Abbildung1: Messung der Ausbreitungsgeschwindigkeiten in Medien | |
| Kurzbeschreibung | |
|---|---|
| Zwei ähnliche Methoden zur Bestimmung der Ausbreitungsgeschwindigkeit in verschiedenen Medien durch Nutzung der elektronischen Laufzeitmessung. | |
| Kategorien | |
| Optik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | SEK II (Einführungsphase; Licht - physikalisch gesehen) |
| Basiskonzept: | System, Wechselwirkung, Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment, Schüler*innenexperiment; Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 2 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Anica Maske |
| Kontakt: | - |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Die Lichtgeschwindigkeit ist eine wichtige Naturkonstante. Vor einigen hundert Jahren versuchte Galileo Galilei (1564 - 1642) diese zu bestimmen, indem über Blendenlaternen an zwei Kilometer entfernten Orten Lichtsignale hin- und hergeschickt und gemessen wurden.[1] Aufgrund der allzu großen Messungenauigkeit dieses Verfahrens schlussfolgerte Galilei schließlich, dass sich Licht unendlich schnell ausbreitet. Erst dem Physiker Fizau (1819 - 1896) gelang es dies mit der präziseren Zahnrad-Methode zu widerlegen. [2] Dieser Eintrag befasst sich mit zwei einfachen Verfahren die Lichtgeschwindigkeit bzw. die Ausbreitungsgeschwindigkeiten in verschiedenen Medien zu bestimmen. Zusätzlich bieten sie die Möglichkeit die Brechungsindizes der Medien zu bestimmen. Im ersten Verfahren werden kurze Lichtimpulse von einem Sender über einen Empfänger registriert und mit einem Oszilloskop dargestellt. In dem anderen Verfahren werden Laserimpulse eines handelsüblichen Laser-Entfernungsmessgeräts ausgesandt und über einen Reflektor wieder aufgefangen. Aus der Phasenverschiebung kann man auf die Lichtlaufzeit schließen.
Der didaktische Schwerpunkt liegt hierbei auf der Bedeutung der Messunsicherheiten, wobei Schüler und Schülerinnen lernen sollen, welche Auswirkungen äußere Einflüsse auf Messverfahren und auf Messergebnisse haben können. Ein grundlegendes Verständnis optischer Strahlengänge ist bei der Durchführung von Vorteil, ebenso wie eine gewisse Vertrautheit mit den elektronischen Geräten.
Inhaltsverzeichnis
Didaktischer Teil
Heutzutage hat der Physikunterricht nicht nur die Aufgabe den Schüler und Schülerinnen physikalisches Fachwissen beizubringen, sondern es soll ein Verständnis entwickelt werden, wie in der Physik Erkenntnisse gewonnen werden und was die zentralen Elemente physikalischen Denkens und Forschens sind. Durch aktives „Physik erleben und betreiben“ sollen sich die Lernenden mit physikalischer Themen kritisch auseinandersetzen und diese reflektieren. (Wiesener et al., 2011/2015 [1]) Experimentieren im Physikunterricht fördert speziell den Kompetenzbereich Erkenntnisgewinnung. Das Erkennen und Einschätzen subjektiver und objektiver Messfehlerquellen sollen erlernt werden, um anschließend die Verlässlichkeit und Tragweite der gewonnen Erkenntnisse beurteilen und bewerten zu können. Außerdem sollen im Anschluss Überlegungen getroffen werden, ob und wie Messfehler minimiert werden können. Da Messunsicherheiten immer und überall auftreten, sind sie von großer Bedeutung für die Interpretation eines Versuchsergebnisses. In einigen Bundesländern wird mittlerweile vom Rahmenlehrplan eine Thematisierung von Messunsicherheiten gefordert und somit als notwendiger Bestandteil des Physikunterrichts gesehen, wie zum Beispiel im Berliner Rahmenlehrplan für die Sekundarstufe I. (Hellwig, 2012, S.11[2])
In den vorgestellten Versuchen zur Bestimmung der Lichtgeschwindigkeit sollen die Schüler und Schülerinnen einfache, bekannte Gesetzmäßigkeiten überprüfen und sich anschließend mit dem Messprozess sowie den gewonnen Ergebnissen kritisch auseinandersetzen. Ein besonders ausschlaggebender Faktor für die Messunsicherheit in diesen Experimenten ist der systematische Fehler, verursacht durch den "Menschen". Obwohl dies eigentlich zu vermeiden gilt, kann auch der Mensch selbst zur Ursache von Messabweichungen werden. (Hellwig, 201, S.61 [2]). So ist besonders auf den Aufbau und die Justierung der verwendeten Geräte zu achten. Die Genauigkeit der horizontalen und vertikalen Ausrichtung der Geräte hat einen erheblichen Einfluss. Besonders der genaue Abstand der Fresnellinse ist zum Reflektor einzuhalten, damit sich die paralell zur optischen Achse einfallenden Strahlen genau auf dem Reflektor schneiden, dem sogenannten Brennpunkt. (Hecht, 2005[3]) Eine weitere einflussreiche Messunsicherheit ist das Ablesen am Oszilloskop aufgrund der Breite des Oszilloskopstrahls. Da die aus den Signalen entstehenden Maxima nicht genau an einem leicht abzulesenden Punkt liegen, ist es nur möglich einen Wert in einem gewissen Bereich abzulesen.
Bei dem Millikan-Versuch treten zum Beispiel ebenso für das Messergebnis entscheidende Messunsicherheiten auf (Beitrag von S. Meisel, 2.02.2017). Um die Öltröpfchen in den Schwebezustand zu kriegen, benötigt der Experimentator viel Fingerspitzengefühl. Ebenso die empfindlichen Gerätschaften tragen dazu bei, dass dies schwer zu erreichen ist. Gelingt es ein Tröpfchen für einen Moment schweben zu lassen, muss der Experimentator schnell und genau ablesen, an welcher Stelle dieser Zustand eingetroffen ist. So treten bei diesem Vorgang (u.a.) durch den „Menschen verursachte“ systematische Fehler, wie das die Ableseungenauigkeit, auf.
Diese Art von Messfehlern sind nicht komplett vermeidbar, aber können durch präzises Arbeiten und ständige Nachkontrolle oder durch Messwiederholungen und „Üben“ sowie durch Verwendung eines mathematischen Korrekturfaktors verringert werden (Hellwig, 2012, S.62[2]).
Damit sich Schülerinnen und Schüler kritisch mit den Unsicherheiten auseinandersetzen können, muss die Lehrperson sie vorab Schritt für Schritt bewusst an diese Problematiken heranführen. Es ist wichtig, dass am Ende eines durchgeführten Messprozesses die Lernenden verstehen, dass keine Messung 100% exakt sein kein.
Am Ende der Messungen sollten die Schüler und Schülerinnen in der Lage sein quantitativ Experimente durchzuführen und auszuwerten. Sie sollen weiterhin ein Verständnis dafür entwickeln, wie mit Hilfe von experimenteller Forschung neues Wissen erlangt werden kann. (Hellwig, 2012, S.5[2])
Versuchsaufbau

Benötigte Materialien, um beide Versuche durchführen zu können:
- Gerätesatz Lichtgeschwindigkeit U8476460 bestehend aus einer Grundeinheit mit enthaltenem Sender (LED mit ca. 30 KHz Pulsfrequenz; 50/ 60 Hz), Empfänger und eingebauter Netzversorgung, Fresnellinse (f = 375 mm) auf Stiel, Triple-Prismen-Reflektor (Mikroprismenspiegel mit einem Durchmesser von ca. 100 mm) auf Stiel sowie 3 gleichlange BNC-Kabel (siehe Betriebsanleitung [3])
- Laser – Entfernungsmessgerät (Firma Bosch DLE 30 Laser plus, siehe Betriebsanleitung [4])
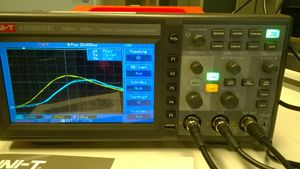
- Oszilloskop (Firma UNI-T UTD2052CEL)
- Stativfüße, - stangen, -klemmen, - platte
- Optische Bank (3 m)
- Ausbreitungsmedien, hier:
- mit Leitungswasser gefüllte Plexiglaswanne (28,8 cm x 15 cm x 13,9 cm; Wanddicke 0,4 cm)
- Acrylglasstab (53,3 cm x 3,4 cm x 3,9 cm)
Die Grundeinheit, die Fresnellinse und der Reflektor werden zur Stabilisierung auf eine optische Bank montiert. Dabei beträgt der Mindestabstand zwischen Grundeinheit und Reflektor 150 cm bei mittiger Linsenstellung. Mit Hilfe des Längeninstruments ist die Entfernung zwischen Grundgerät (Ausgangspunkt ist der Strahlteiler, welcher auf dem Gehäuse der Grundeinheit abgebildet ist) und Reflektor bestimmbar. Die minimale Entfernung von Grundeinheit und Linse (Abstand a) ist etwa f (Brennweite der Linse). Die Entfernung Linse und Reflektor (Abstand b) wäre im Fall a=f unendlich. Über die Formel b= (af)/(a-f) ist die korrekte Position der Linse zu berechnen. Um möglichst optimale Ergebnisse zu erhalten, ist es ratsam auf die Genauigkeit der horizontalen und vertikalen Ausrichtung der Geräte zu achten. Das Oszilloskop wird mit der Grundeinheit über BNC-Kabel, gleicher Länge und Impendanz, wie folgt verbunden:
- Ausgang „A“ der Grundeinheit mit Kanal „CH1/X“ vom Oszilloskop (Lichtlaufzeit zwischen Sender, Reflektor und Empfänger)
- Ausgang „B“ der Grundeinheit mit Kanal „CH2/Y“ vom Oszilloskop (Referenzsignal)
- Ausgang „C“ der Grundeinheit mit Kanal „EXTTrig“ vom Oszilloskop (Strahltriggerung)
Folgende Einstellungen müssen am Oszilloskop vorgenommen werden um die gewünschte Darstellung zu erhalten.
- Mode: Zweikanalbetrieb (Einschalten der Kanäle CH1 und CH2) mit kleiner gleich 100 mV/ DIV
- Ablenkung in ns/ DIV, zum Beispiel 5 ns/ DIV(Über „F3“ und „Scale“ kann von der groben Ablenkungseinstellung in die Feineinstellung gewechselt werden.)
- Triggerung extern
Eventuell müssen die Linse und der Reflektor nach erstmaligen Einschalten der Grundeinheit erneut justiert werden, um einen möglichst hohen Anteil an reflektierten Lichts zu empfangen. Dabei sollte das Empfängersignal auf dem Oszilloskop beobachtet werden, um die Ausrichtung weiter zu optimieren. Hilfreich ist hierbei ein Blick aus der Position des Grundgerätes auf den Reflektor, wobei bei einer optimalen Einstellung der fokussierte Lichtstrahl auf dem Reflektor zu sehen ist. Bis zu einer Entfernung von ca. 8 m wird der rot erscheinende Leuchtfleck gut sichtbar abgebildet.
Mit dem beschriebenen Aufbau lässt sich ebenso die Lichtgeschwindigkeit in den Medien Wasser und Acrylglas bestimmen, wobei das Medium auf eine Stativplatte auf der optischen Bank zwischen Linse und möglichst nah an dem Reflektor montiert wird. Die Wasserwanne sowie das Acrylglas werden längs in den Strahlengang gebracht. Die Wasserwanne wird bis unter den Rand mit Leitungswasser gefüllt. In diesem Versuch betrug die Wasserhöhe ca. 10 cm.
Zum Vergleich kann eine vereinfachte Methode zur Messung der Ausbreitungsgeschwindigkeit in Leitungswasser und Acrylglas unter Verwendung eines Laser-Entfernungsmessgeräts durchgeführt werden. Das Laser-Entfernungsmessgerät wird so genau wie möglich entlang einer dünnen Linie parallel zu einer Wand (o.ä.) ausgerichtet, wobei die Laseröffnung zur Wand zeigt. Das Medium wird direkt vor den Strahlengang gebracht.
Vgl. mit Versuchsbeschreibung leybold [5]
Versuchsdurchführung
Nach Abschluss des Aufbaus sollte zuerst mit dem Laser-Entfernungsmessgerät die Entfernung zwischen Grundeinheit und Reflektor bestimmt sowie die Linse auf den entsprechenden Abstand zwischen Grundeinheit- Linse bzw. Linse-Reflektor gebracht werden. Nach Einschalten der Geräte müssen die entstandenen Signale(„B“ Referenzsignal und „A“ Lichtlaufzeit) im Oszilloskop so positioniert werden, dass zum Ablesen der Verzögerungszeit sich ihre beiden Maxima auf gleiche Höhe befinden. Dies ist möglich über die Räder „Position“, wobei die Vertikale so eingestellt wird, dass beide Signale möglichst genau symmetrisch zu mittleren Horizontallinie des Schirms sind und über die Feinstellung ihre Maxima genau auf derselben Horizontallinie liegen. Beide Signale werden über den Phasenverschieber möglichst genau zur Deckung gebracht sind. Nach geeigneter Position der Signale wird nun der Abstand der Maxima, welcher der Zeitdifferenz entspricht, abgelesen. Es sollten mehrere Messwiederholungen mit unterschiedlichen Abständen b durchgeführt werden, „um Auskunft über die mit ihnen verbundenen Unsicherheiten zu erhalten“ (Hellwig, 2012 S.18 [2]). Später können die Mittelwerte der jeweiligen Messungen je Medium bestimmt werden. Um präzise Ergebnisse zu erhalten, sollte grundsätzlich vor jeder Messung die Genauigkeit der Justierung überprüft. (siehe Versuchsbeschreibung leybold [6])
Bei der Methode mit dem Laser-Entfernungsmessgerät muss darauf geachtet werden, dass das Messgerät während der Messung nicht bewegt wird. Nach Drücken des Knopfes auf dem Messgerät zur Längenmessung erscheint nach ca. 0,5 s das Ergebnis.
Vgl. mit Versuchsbeschreibung leybold [7]
Messergebnisse
In der Tabelle 1 sind die Messergebnisse für die Bestimmung der Ausbreitungsgeschwindigkeiten in den Medien Wasser, Acrylglas und Luft dargestellt.
| Messung Nr. | Medium | Strecke d in m | Zeitdifferenz ∆t in ns |
|---|---|---|---|
| 1 | Wasser | 0,28 | 3 |
| 2 | Wasser | 0,28 | 2 |
| 3 | Wasser | 0,28 | 3 |
| 4 | Acrylglas | 0,635 | 6 |
| 5 | Acrylglas | 0,635 | 5 |
| 6 | Acrylglas | 0,635 | 5 |
| 7 | Licht | 1,624 | 9 |
| 8 | Licht | 1,774 | 10 |
| 9 | Licht | 2,019 | 12 |
| 10 | Licht | 2,524 | 14 |
| 11 | Licht | 2,763 | 16 |
In der Tabelle 2 sind die Messergebnisse, welche über die Methode mit dem Laser-Entfernungsmessgerät aufgenommen wurden, einzusehen.
| Messung Nr. | Medium | Strecke d ohne Medium in m | Strecke d mit Medium in m |
|---|---|---|---|
| 12 | Wasser | 0,468 | 0,573 |
| 13 | Wasser | 0,874 | 0,554 |
| 14 | Wasser | 1,158 | 0,581 |
| 15 | Acrylglas | 0,53 | 1,141 |
| 16 | Acrylglas | 0,814 | 1,144 |
| 17 | Acrylglas | 1,782 | 1,139 |
Auswertung der Messergebnisse
Über das einfache Weg-Zeit-Gesetz (1) kann die Ausbreitungsgeschwindigkeit sowie der Brechungsindex über (2) bestimmt werden. Um die Zeitdifferenz im Medium Wasser oder Acrylglas zu erhalten, müssen die Zeiten sowohl mit, als auch ohne Medium gemessen werden.
Es ergeben sich während der Messung verschiedene rechnerisch einzubeziehende Messunsicherheiten. Das Laserentfernungsmessgerät misst Strecken bis auf eine Abweichung von 0,005 m genau. Die Ableseunsicherheit am Oszilloskop wurde auf eine Abweichung von 2 ns geschätzt, welche durch die Breite der Signalmaxima bestimmt wird. Da sich diese Abweichung im selben Zeitbereich befindet wie die gemessenen Zeitdifferenzen, wird dadurch die sich ergebene Unsicherheit der Ausbreitungsgeschwindigkeit bzw. Brechungsindex der Medien Acrylglas und Leitungswasser sehr hoch sein.
In den Tabellen 3 und 4 sind die Berechnungen unter Verwendung der Formel (1) und (2) sowie deren Unsicherheiten dargestellt. Es ist hierbei drauf zu achten, dass die gemessene Strecke d mal zwei multipliziert wird, da der Laserstrahl die Strecke d hin und zurück läuft. Die Unsicherheiten ucMedium sowie unMedium werden nach den Formeln für die Fehlerfortpflanzung von Unsicherheiten unkorrelierter Größen berechnet (vgl. Müller, 2007, S. 36 Formel (30), (31)[8]).
| Messung Nr. | Medium | Ausbreitungsgeschwindigkeit cMedium *10^6 m/s | Unsicherheit ucMedium *10^6 m/s | Brechungsindex nMedium | Unsicherheit unMedium |
|---|---|---|---|---|---|
| 1 | Wasser | 192,00 | 259,33 | 1,75 | 2,59 |
| 2 | Wasser | 288,00 | 581,00 | 1,17 | 5,81 |
| 3 | Wasser | 192,00 | 259,33 | 1,75 | 2,59 |
| 4 | Acrylglas | 117,67 | 120,11 | 1,58 | 1,73 |
| 5 | Acrylglas | 213,20 | 172,56 | 1,89 | 1,20 |
| 6 | Acrylglas | 213,20 | 172,56 | 1,89 | 1,20 |
| Messung Nr. | Ausbreitungsgeschwindigkeit cMedium *10^6 m/s | Unsicherheit ucMedium *10^6 m/s | Brechungsindex nMedium | Unsicherheit unMedium |
|---|---|---|---|---|
| 7 | 360,89 | 81,31 | 0,81 | 0,19 |
| 8 | 354,80 | 71,96 | 0,85 | 0,17 |
| 9 | 336,50 | 56,92 | 0,89 | 0,15 |
| 10 | 360,57 | 52,22 | 0,83 | 0,12 |
| 11 | 345,38 | 43,80 | 0,87 | 0,11 |
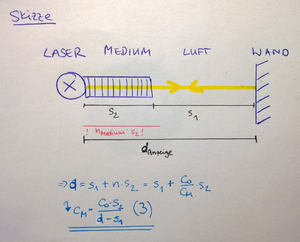
In der Tabelle 5 sind die berechneten Ausbreitungsgeschwindigkeiten in den Medien Wasser und Acrylglas unter Verwendung des Laser-Entfernungsmessgeräts einzusehen. Um mit dem Laser-Entfernungsmessgerät die Ausbreitungsgeschwindigkeit zu bestimmen, wird die in Abbildung 5 dargestellte Formel (3) verwendet, allerdings unter Voraussetzung, dass die Lichtgeschwindigkeit c0 bekannt ist. Zu beachten ist, das die Strecken wieder mal zwei multipliziert werden müssen. Auch hier werden die Unsicherheiten unter Nutzung der Fehlerfortpflanzung unkorrelierter Größen verwendet (vgl. Müller, 2007, S. 36, Formel (30), (31) [9]).
| Messung Nr. | Medium | Ausbreitungsgeschwindigkeit cMedium *10^6 m/s | Unsicherheit ucMedium *10^6 m/s | Brechungsindex nMedium | Unsicherheit unMedium |
|---|---|---|---|---|---|
| 12 | Wasser | 219,68 | 4,70 | 1,3 | 0,03 |
| 13 | Wasser | 308,36 | 5,5 | 0,97 | 0,02 |
| 14 | Wasser | 298,76 | 3,88 | 1,03 | 0,01 |
| 15 | Acrylglas | 280,08 | 1,31 | 1,07 | 0,01 |
| 16 | Acrylglas | 549,10 | 9,89 | 0,55 | 0,01 |
| 17 | Acrylglas | 235,15 | 2,83 | 1,27 | 0,02 |
| Medium | Ausbreitungsgeschwindigkeit in 10^6 m/s | Brechungsindex n |
|---|---|---|
| Wasser | 225, 40 | 1,33 |
| Acrylglas | 200,93 | 1,49 |
| Luft | 299,79 | 1 |
In den Tabellen 7 und 8 sind die jeweiligen Mittelwerte der errechneten Ausbreitungsgeschwindigkeit und Brechungsindizes einzusehen.
| Medium | Ausbreitungsgeschwindigkeit mit den Unsicherheiten in 10^6 m/s | Brechungsindex n mit den Unsicherheiten |
|---|---|---|
| Wasser | 275,6 ± 4,69 | 1,1 ± 0,02 |
| Acrylglas | 354,78 ± 4,68 | 0,96 ± 0,01 |
| Luft | 351,63 ± 56,92 | 0,84 ± 0,14 |
| Medium | Ausbreitungsgeschwindigkeit mit den Unsicherheiten in 10^6 m/s | Brechungsindex n mit den Unsicherheiten |
|---|---|---|
| Wasser | 224 ± 366,55 | 1,75 ± 3,66 |
| Acrylglas | 181,36 ± 155,07 | 1,38 ± 1,38 |
| Luft | 351,63 ± 56,92 | 0,84 ± 0,14 |
Diskussion
Passend zum didaktischen Schwerpunktthema Messunsicherheiten, wirken sich in diesem Versuch die Unsicherheiten erheblich auf die Messergebnisse aus. Ein gutes Beispiel um Gesetzmäßigkeiten zu überprüfen und Zusammenhänge klar zu machen, ohne exakte Messergebnisse zu erhalten. Wie in Tabelle 4 (Mittelwertberechnungen in Tabelle 8) zu sehen, liegen die Messergebnisse für das Medium Luft jeweils mit ihren Fehlerintervallen nahe an den Referenzwerten. Bei Betrachtung der Ergebnisse für die Medien Wasser und Acrylglas (vgl. Tabelle 3 und 8) sieht es zwar so aus, dass die Messergebnisse im Vergleich mit dem Referenzwert in einem guten Bereich liegen, aber aufgrund des zu hohen Fehlerintervalls ist darüber keine genaue Aussage zu treffen möglich. Dies liegt an dem hohen Einfluss der Ableseunsicherheit. So hat diese Unsicherheit weniger Einfluss im Medium Licht, aber umso mehr in den anderen beiden. Das liegt an der Berechnung der Unsicherheiten nach der Methode der Fehlerfortpflanzung. Um diesen Fehler in zukünftigen Messungen zu verringern, könnte möglicherweise die Verwendung periodischer statt kurzer Lichtimpulse einen positiven Effekt beitragen. Die sich auf dem Oszilloskop ergebene Sinuskurven könnte bei der Ablesung der Zeitdifferenz vorteilhafter sein. Es können noch weitere Ursachen für die Messunsicherheiten genannt werden. Der Versuchsaufbau ist zwar recht simpel, allerdings sehr empfindlich. Eine nicht genaue Justierung und Einhaltung der exakten Position der Geräte, insbesondere der Medien, führt zu einer Veränderung des Brechungswinkels und des Fokus. Besonders schwierig ist es die exakte, zum Strahlengang parallele Position der Medien beizubehalten. Kleinste Ungenauigkeiten wirken sich auf die Messung aus. Ein weiterer Messfehler könnte aufgrund der kaum bemerkbaren Wellenbewegungen im Wasser entstanden sein, verursacht durch äußere Erschütterungen.
Die Bestimmung der Ausbreitungsgeschwindigkeit in Medien mit Hilfe eines handelsüblichen Laser-Entfernungsmessgeräts erscheint eine sowohl einfachere umzusetzende sowie auch präzisere Methode zu sein. So sind die Fehlerintervalle der Unsicherheiten passend zu den Ergebnissen und schließen die Referenzwerte mit ein (vgl. Tabelle 7). Die rechnerischen, systematischen Unsicherheiten werden hier nur durch das Laser-Entfernungsmessgerät verursacht. Ableseunsicherheiten, wie bei der anderen Methode, welche die Messergebnisse ungenauer machen lässt, treten hier nicht auf. Interessant ist das Ergebnis der Messung Nr. 16. Offensichtlich gibt es hier keinen Bezug zum Referenzwert und passt auch sonst nicht zu den Ergebnissen in der Tabelle 5. Einflussreiche, allerdings nicht rechnerisch mit einbezogene Aufbaufehler könnten hier die Ursache für sein. Um genaue Ergebnisse zu erhalten, muss der Laserstrahl senkrecht auf das Medium treffen. Da hier nur mit bloßem Auge gearbeitet wurde, empfiehlt es sich stattdessen mit entsprechenden Hilfsmitteln, wie Millimeterpapier oder Winkelmessern, zu arbeiten. Mehrere Messwiederholungen würden das Ergebnis präziser machen. Das gesetzte didaktische Ziel ist erreicht worden. Schülerinnen und Schüler führen die Experimente (ggf.) selbstständig durch und werten diese aus. Sie lernen, dass es keine exakte Messung gibt. Unerwartete Messergebnisse fördern das selbstständige und vor allem kritische Denken und regen zu Lösungen an. Das Verständnis physikalischen Denkens und Forschens wird durch das „aktive Physik-Erleben“ intensiver gefördert und jeder Lernende wird aufgefordert selber ein Forscher zu sein.
Sicherheitshinweise
Da es sich hier um einen Versuch mit elektrischen Geräten handelt, ist im Vorhinein zu prüfen, ob die Geräte sicherheitsgemäß funktionstüchtig sind und alle untereinander korrekt verschaltet sind. Der Experimentator sowie alle weiteren Teilnehmer dürfen nicht direkt in den Laserstrahl gucken - auch nicht mit einem Fernglas oder einer Brille. Den Laserstrahl nicht auf Menschen richten
Literatur
- ↑ Wiesner, Hartmut; Schecker, Horst; Hopf, Martin: „Physikdidaktik kompakt” Aulis Verlag, 2011/ 2015
- ↑ 2,0 2,1 2,2 2,3 2,4 Hellwig, Julia "Dissertation: Messunsicherheiten verstehen - Entwicklung eines normativen Sachstrukturmodells am Beispiel des Unterrichtsfaches Physik" Bochum 2012
- ↑ Hecht, Eugene: "Optik" Oldenbourg Wissenschaftsverlag, 4. Auflage 2005
Siehe auch
- Sennewald, Planetwissen: Galileo Galilei ; http://www.planet-wissen.de/technik/weltraumforschung/astronomie/pwiegalileogalilei100.html [31.03.2017]
- Geboren am: Hippolyte Fizeau ; https://geboren.am/person/armand-hippolyte-louis-fizeau [31.03.2017]
- leybold: Versuchsbeschreibung von leybold ; https://www.leybold-shop.at/vp5-6-3-2.html [31.03.2017]
- Manualzz: Betriebsanleitung Gerätesatz Lichtgeschwindigkeit U8476460 https://manualzz.com/doc/8802897/u8476460-230--1000882- [31.03.2017]
- Conrad: Betriebsanleitung Laser – Entfernungsmessgerät http://www2.produktinfo.conrad.de/datenblaetter/800000-824999/811691-an-01-de-Laser_Entfernungsmesser_DLE_30_plus.pdf [31.03.2017]