Bestimmung der Leistungszahl einer Wärmepumpe
| Bestimmung der Leistungszahl einer Wärmepumpe | |
 Abb. 1: Demonstrationsmodell einer Wärmepumpe | |
| Kurzbeschreibung | |
|---|---|
| Das Experiment veranschaulicht qualitativ den Kreisprozess, der die Funktionsweise einer Wärmepumpe, und umgedreht auch die, eines Külschrankes erklärt. Durch Messung der Temperaturen und der elektrischen Leistung kann zusätzlich die Leistungszahl berechnet werden. | |
| Kategorien | |
| Thermodynamik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | System, Energie |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment |
| Anspruch des Aufbaus | leicht, Modell muss vorhanden sein |
| Informationen | |
| Name: | Sarah Heydemann |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Mit Hilfe dieses Experimentes wird die Funktionsweise zweier wichtiger Alltagsgeräte veranschaulicht, die der Wärmepumpe und des Kühlschrankes. Wärmepumpen dienen in vielen Haushalten der Erzeugung von Wärme zum Heizen, indem durch mechanische Arbeit thermische Energie aus einem Bereich entzogen und in einem anderen zugeführt wird. Das gleiche Prinzip findet umgekehrt auch zum Kühlen, nämlich bei einem Kühlschrank, Anwendung. Das Experiment eignet sich nicht nur zum Kennenlernen des Kreisprozesses, der die Funktionsweise von Kühlschrank und Wärmepumpe erklärt, sondern kann durch gezielte Temperaturmessungen auch dafür verwendet werden, die Leistungszahl zu berechnen. Diese gibt das Verhältnis aus zugeführter mechanischer Arbeit und erzeugter thermischer Energie an und kann als thermischer Wirkungsgrad unter bestimmten Betriebsbedingungen verstanden werden.
Inhaltsverzeichnis
Didaktischer Teil
In diesem Abschnitt sollen auf didaktischer Ebene die Alltagsvorstellungen von Schülerinnen und Schülern zum Wärme- und Kältebegriff thematisiert werden. Diese Begriffe verwendet wohl jeder Schüler in seinem Alltag, ohne sich darüber bewusst zu sein, was sie physikalisch eigentlich bedeuten. Gibt man beispielsweise das Wort „Kälte“ in die Suchmaschine „Google“ ein, so kommt als erstes der aktuelle Wetterbericht. Dies ist ein erstes Anzeichen, dass zur typischen Fehlvorstellung der Schüler führt, Wärme als hohe Temperatur und Kälte als niedrige Temperatur aufzufassen. Ein weiterer physikalischer Begriff, der eng mit einer Vorstellung zu Wärmeerscheinungen einhergeht, ist die Energie. Wie auch Kircher in seinem Buch schreibt ([1] (2002), S. 16), ist es „uns selbstverständlich, dass sich Dinge von allein […] nur abkühlen, aber sich nie von allein erwärmen.“ Dabei muss aber beachtet werden, dass der sich abkühlende Körper eine Temperatur oberhalb der Umgebungstemperatur haben muss. Wärme ist also etwas, „das von einem warmen zu einem kalten Gegenstand fließt“, was eben in der Physik mit dem Begriff Energie abgegrenzt wird. Kircher unterscheidet weiterhin diese beiden Begriffe in einen extensiven Aspekt (Wärme) und einen intensiven Aspekt (Energie). „Intensive Größen stehen dafür, „wie stark“ etwas ist […]. Extensive Größen geben an, „wie viel“ vorhanden ist.“
Das nächste Dilemma findet sich nun im Begriff der Kälte selbst, der in den Fachterminus der Physik keinen Einzug gefunden hat. Reinders Duit ([2] (2011), S. 195) schreibt in seinem Kapitel zu Wärmevorstellungen: „Wärme und Kälte sind Gegensätze auf einer Dimension, die durch die Temperatur aufgespannt wird.“ Kann der Begriff Kälte also als Negation des Begriffs Wärme angenommen werden und ist es daher unnötig beide eigenständig zu definieren? Genauso müsste Kälte in Bezug auf den Energiebegriff dann etwas sein, das von einem kalten zu einem warmen Gegenstand fließt.
Viele Schülerinnen und Schüler werden mit jenen Alltagsvorstellungen in den Unterricht kommen und müssen diese Vorstellungen in Richtung der physikalischen Grundbegriffe erst noch entwickeln. Für den Unterricht schlägt Kircher daher vor, erst einmal das Prinzip des Temperaturausgleichs über unser Wärmeempfinden klar zu machen. Warum fühlen sich Dinge gleicher Temperatur als ungleich warm an? Über die Erfahrung dass sich Temperaturdifferenzen stets ausgleichen, gelange man schließlich zum Energiebegriff (Wärme als Prozessgröße). Woraus „der Grundstein für das Verständnis des 2. Hauptsatzes“ gelegt wird.
Funktion einer Wärmepumpe
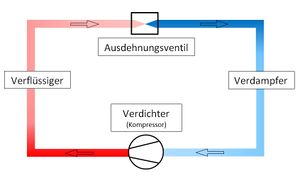
An dieser Stelle soll der Kreisprozess einer Wärmepumpe beschrieben werden, der in Abbildung 2 schematisch zu sehen ist. Die Bezeichnungen der vier Bauteile (Kompressor, Verflüssiger, Ausdehnungsventil und Verdampfer) finden sich auch auf dem Demonstrationsmodell wieder.
Die Wärmepumpe besteht aus einem Metallrohr, das mit einem geeigneten verflüssigbarem Gas, auch Kältemittel genannt, befüllt ist. Geeignet bedeutet, dass das Gas einen passenden Siedepunkt hat, also bei ausreichend niedrigem Druck verdampft und bei ausreichend hohem Druck kondensiert. Laut Angabe auf dem Modell handelt es sich um R-12 (Dichlordifluormethan) als Kältemittel. Dieses wurde aber als Kältemittel verboten, da es die Ozonschicht zerstört. Häufig als Kältemittel verwendet wird daher heutzutage R134a (Tetrafluorethan)[3].
Der Kompressor komprimiert das Gas, indem der Druck erhöht wird, wodurch die Temperatur des Kältemittels im Metallrohr steigt. Im Verflüssiger kondensiert das Gas nun durch Abgabe von Wärme an das Wasser im Verflüssigergefäß. Anschließend folgt das Ausdehnungsventil (Abb. 3), welches durch seine technische Funktionsweise dafür sorgt, dass die Temperatur des flüssigen Kältemittels stark sinkt. Als letztes folgt der Verdampfer, in dem das Fluid durch Aufnahme von Wärme wieder in den gasförmigen Zustand über geht. Das Gas wird nun im Kompressor wieder komprimiert und der Kreislauf beginnt erneut.
Als Ergebnis kann man also die Temperaturänderungen des Wassers im Verflüssigergefäß (Erwärmung) und im Verdampfergefäß (Abkühlung) beobachten. In Betrieb wurde im Verflüssiger ein Druck von und im Verdampfer ein Druck von angezeigt, welche aber mit laufender Messung leicht zunahmen.
Versuchsanleitung
Aufbau
Für das Experiment wurde ein vorgefertigtes Modell der Firma "Müller Lehrtechnik" (Modell WP 8788, Type: 1502) verwendet (Siehe Abb. 1). Im Internet sind weder der Hersteller, noch Produkte von ihm zu finden, so dass davon ausgegangen werden kann, dass es sich um ein älteres Modell handelt. Lediglich der Kompressor der Marke "Danfoss" wurde vermutlich erneuert. Als Alternative haben auch führende Lehrmittelhersteller wie Leybold (389521) und Phywe Wärmepumpenmodelle im Sortiment.
Zur Messung werden weiterhin zwei Wassereimer, mit einem Volumen von je einem Liter, sowie zwei Thermometer benötigt. Dafür wurden die Temperaturfühler der Firma Leybold (666193) verwendet. Um später die Leistungszahl berechnen zu können, ist es nötig, die elektrische Leistung des Kompressors zu kennen. Um diese zu messen, wurde das Joule- und Wattmeter der Firma Leybold (531831) benutzt, das mit Hilfe eines Messanschlusskastens, ebenfalls von Leybold (50205), vorgeschaltet wird.
Durchführung
Bevor die Wärmepumpe in Betrieb genommen werden kann, müssen die beiden Behälter mit je einem Liter Wasser befüllt werden. Diese werden so aufgestellt, dass das Wasser die spiralförmig angeordneten Metallrohre komplett umschließt. Mit Hilfe der Temperaturfühler wird die Temperatur in beiden Gefäßen gemessen. Nun wird über den Schalter die Pumpe angeschaltet. Gleichzeitig muss eine Stoppuhr gestartet werden, da nun in regelmäßigen Abständen die Wassertemperaturen in beiden Gefäßen gemessen werden müssen. Für die spätere Auswertung ist es ausreichend, die Temperatur jede Minute einmal zu messen. Wichtig ist es das Wasser während der Messung kontinuierlich umzurühren, um für eine homogene Mischungstemperatur zu sorgen, da anderenfalls die Messung stark verfälscht werden kann. Auch sollte man bei der Temperaturmessung darauf achten mit dem Temperaturfühler nicht das Metallrohr zu berühren.
Das Leistungsmessgerät kann während der Messung ab und zu beobachtet werden, um sicher zu gehen, dass die Leistung einen in etwa konstanten Wert annimmt. Bei meinen Versuchen schwankte die elektrische Leistung um ein bis zwei Watt, was später als Messunsicherheit festgelegt wurde.
Nach zehn minütiger Messung wird das Gerät wieder abgeschaltet.
Ergebnisse
Wie zu erwarten war, stieg die Wassertemperatur im Verflüssigergefäß kontinuierlich an. Im Verdampfergefäß fiel sie ebenso kontinuierlich ab. Wie bereits erwähnt, wurden jede Minute die Temperaturen im Verdampfer- und Verflüssigergefäß gemessen. Es ergaben sich folgende Messwerte:
Messwerttabelle Wärmepumpe
| Zeit in min | Temperatur Verdampfer in °C | Temperatur Verflüssiger in °C |
|---|---|---|
| 0 | 21,3 | 22,7 |
| 1 | 19,4 | 24,3 |
| 2 | 17,1 | 26,5 |
| 3 | 14,6 | 28,8 |
| 4 | 12,1 | 31,1 |
| 5 | 10,2 | 33,9 |
| 6 | 8,2 | 35,8 |
| 7 | 6,3 | 37,8 |
| 8 | 4,8 | 39,8 |
| 9 | 3,6 | 41,5 |
| 10 | 2,7 | 43,7 |
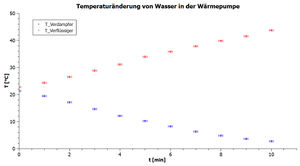
Eine grafische Darstellung der Messwerte ist in Abbildung 4 zu finden und wurde mit dem Programm QtiPlot erstellt. Wie in der Legende beschrieben, ist die steigende Temperatur im Verflüssigergefäß in rot und die sinkende Temperatur im Verdampfergefäß in blau dargestellt. Die Größe der Unsicherheiten wurde abgeschätzt. Darauf wird im folgenden Kapitel "Auswertung" noch einmal Bezug genommen.
Für die Berechnung der Leistungszahl sind in folgender Auflistung noch einmal alle relevanten Messwerte und Konstanten aufgeführt:
- Anfangstemperatur Verdampfer:
- Anfangstemperatur Verflüssiger:
- Endtemperatur Verdampfer:
- Endtemperatur Verflüssiger:
- Versuchsdauer:
- Elektrische Leistung:
- Wassermenge:
- Spez. Wärmekapazität Wasser: [4]
Warum mehrere Messwerte in kleinen Zeitintervallen aufgenommen wurden, obwohl für die Berechnung der Leistungszahl nur die Anfangs- und Endtemperatur von Nöten sind, wird im letzten Absatz der Auswertung geklärt.
Auswertung
Die schon bei der Auflistung der Messergebnisse angegebenen Unsicherheiten wurden abgeschätzt. Bei der Temperatur schwankten die Werte immer ein wenig. Außerdem kann trotz des Rührens nicht hundertprozentig von einer homogenen Mischungstemperatur ausgegangen werden. Bei der Zeitmessung wurden fünf Sekunden angenommen, da beide Temperaturen nicht exakt zeitgleich abgelesen werden konnten. Bei der Leistung gab es auch leichte Schwankungen, als Unsicherheit wurde daher das letzte Digit angenommen. Weitere Unsicherheiten, die nun bei der Berechnung auftreten, ergeben sich jeweils nach Gaußscher Fehlerfortpflanzung wie folgt:
- .
Für die Leistungszahl muss zunächst die aufgenommene Wärmemenge des Wassers im Verflüssigergefäß berechnet werden. Dazu wird zunächst die Temperaturdifferenz im Verflüssiger berechnet:
Es ergibt sich daraus die aufgenommene Wärmemenge des Wassers im Verflüssigergefäß zu:
- .
Diese wird für die Berechnung der Leistungszahl nun ins Verhältnis zu der vom Kompressor aufgewendeten elektrischen Arbeit gesetzt, welche sich wie folgt ergibt:
Die Leistungszahl ergibt sich nun also aus dem Verhältnis von aufgenommener Wärmemenge im Verflüssigergefäß und vom Kompressor aufgewendeter elektrischer Arbeit zu:
Herkömmliche Wärmepumpen können eine Leistungszahl zwischen drei und sechs erreichen[5]. Es ist zu erkennen, dass die im Experiment ermittelte Leistungszahl, auch innerhalb der Unsicherheiten, deutlich unterhalb dessen liegt. Es stellt sich also die Frage, wie man die Messung optimieren kann. Eine Möglichkeit wäre es, die Metallrohre, sowie die Wasserbehälter thermisch zu isolieren. Somit würde weniger Wärme an die Umgebung abgegeben, beziehungsweise aus der Umgebung aufgenommen werden. Eine weitere Möglichkeit wäre es, den Kompressor erst einmal auf Betriebstemperatur zu bringen, sprich ihn etwa zehn Minuten laufen zu lassen, anschließend das Wasser in den Behälter zu erneuern und erst dann die Messung zu starten.
Mit eben diesen beiden Optimierungen wurde die Messung erneut durchgeführt. Die thermische Isolierung wurde durch eine einige Millimeter dicke Zeitungspapierschicht und eine darüberliegende Schicht aus Alufolie realisiert (siehe Abb. 5). Durch das Zeitungspapier wird hauptsächlich die Wärmeleitung an die Umgebung abgeschirmt, mit der Alufolie soll die Wärmestrahlung eingeschränkt werden. Der Kompressor lief zehn Minuten vor der Messung warm. Es ergaben sich nach analoger Messung wie zuvor, folgende Temperaturen im Verflüssigergefäß:
- Anfangstemperatur Verflüssiger (mit Isolation):
- Endtemperatur Verflüssiger (mit Isolation):
Es ist zu erkennen, das mit der thermischen Isolierung eine größere Temperaturdifferenz erreicht wurde, so dass auch eine größere Leistungszahl zu erwarten ist. Nach analoger Rechnung wie zuvor, ergibt sich nun eine Leistungszahl von:
Dies ist ein deutlich besseres Ergebnis, dennoch liegt die Leistungszahl, auch innerhalb ihrer Unsicherheiten, immernoch weit entfernt von der angegebenen Lesitungszahl herkömmlicher Wärmepumpen. Ein Grund dafür ist vermutlich, dass die Wasserbehälter nach oben hin nicht verschlossen (isoliert) werden konnten, da eine Öffnung zum Rühren und zum Messen der Temperatur benötigt wird.
Die Versuchsdauer von zehn Minuten wurde mehr oder minder frei gewählt. Eine Versuchsdauer von 7 Minuten oder 13 Minuten wären beispielsweise ebenso denkbar.
Da Messwerte in einminütigen Zeitintervallen aufgenommen wurden, könnte die Rechnung theoretisch für jedes beliebiege Zeitintervall innerhalb der zehn Minuten durchgeführt werden. Lediglich die Temperaturdifferenz und die Versuchsdauer müsste in der Rechnung jeweils ersetzt werden. Beim Betrachten der grafischen Darstellung lässt sich aber vermuten, dass die Temperaturen sich einem Grenzwert anzunähern scheinen. Das heißt, dass sie sich mit zunehmender Messzeit nicht mehr groß verändern, was sich durch die Annäherung an die Grenze zum Aggregatzustandswechsel des Wassers bei 0°C im Verdampfergefäß erklären lässt. Ebenso steigt bei zunehmender Temperaturdifferenz zwischen den Gefäßen und der Umgebung die Aufnahme beziehungsweise Abgabe der Wärme aus bzw. an die Umgebung. Es ergibt sich also logisch daraus, dass die Berechnung der Leistungszahl in dieser Phase stark verfälscht würde, so dass von einer solchen abzuraten ist. Bei der vorliegenden Messung (ohne thermische Isolation) ergaben sich bei Temperaturdifferenzen zwischen allen zehn Messzeitpunkten und der Starttemperatur jeweils Leistungszahlen in der gleichen Größenordnung (etwa zwischen 1,3 und 1,4), so dass ein nur zufällig richtiges Ergebnis auszuschließen ist.
Ein weiterer bisher unbeachteter Aspekt ist, dass zur Berechnung der Leistungszahl die aufgenommene Wärme im Verflüssigergefäß verwendet wurde. Wie schon erwähnt, gilt das umgekehrte Prinzip der Wärmepumpe für die Funktionsweise eines Kühlschrankes. Um dessen Leistungszahl zu bestimmen, kann man sich also das Verhältnis aus abgegebener Wärme im Verdampfergefäß und aufgewendeter elektrischer Arbeit anschauen. Beim Betrachten der Grafik der Messergebnisse (Abb. 4) fällt auf, dass die beiden Temperaturkurven scheinbar symmetrisch zu einer horizontal verlaufenden Mittelachse verlaufen. An dieser Stelle wird sichtbar, wofür es notwendig ist, mehrere Messwerte in kleinen Zeitintervallen aufzunehmen. Denn nur so kann eine klare Antwort auf die Frage gefunden werden, ob beide Temperaturkurven, und damit auch die Prozesse des Erwärmens und Kühlens, symmetrisch verlaufen. Ein reines betrachten der Temperaturdifferenz zwischen Anfang und Ende, die etwa gleichgroß sein sollte, wie die Temperaturdifferenz im Verflüssiger, könnte auch Zufall sein. Sie könnte beispielsweise nur in diesem Messzeitpunkt zufällig übereinstimmen, zu anderen Messzeitpunkten aber völlig verschieden sein.
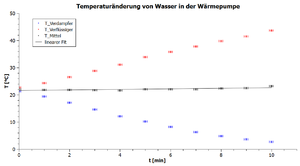
Um dies nun zu testen, wurde das arithmetische Mittel aus jedem Messwertpaar eines Zeitpunktes gebildet und zusätzlich in die Grafik eingefügt (siehe Abb. 6). Mit Hilfe des Programms QtiPlot wurde nun ein linearer Fit durch diese berechneten Mittelwerte gelegt. Das Programm gab folgende Funktionsgleichung für diese lineare Funktion aus:
Es ist zu erkennen, dass die Steigung der linearen Funktion innerhalb der Unsicherheiten in etwa Null ist, so dass die Annahme einer horizontalen Symmetrieachse bestätigt werden kann. Daraus wiederum lässt sich nun schließen, dass die Temperaturzunahme im Verflüssigergefäß analog zur Temperaturabnahme im Verdampfergefäß abläuft. Berechnet man also die Leistungszahl über die Abnahme der Temperatur im Verdampfergefäß, so sollte diese genau gleich groß sein.
Fazit
Das Experiment brachte die gewünschten Ergebnisse. Die gemessenen Temperaturen in den Wassergefäßen verhielten sich wie gewünscht und es konnte eine passable Leistungszahl errechnet werden. Optimierungen am Versuch und weiterführende Überlegungen, wie die Umkehrung des Prinzips der Wärmepumpe zum Prinzip des Kühlschrankes wurden kurz erwähnt und können im Unterricht weiter diskutiert werden. In Bezug auf den didaktischen Teil kann mit diesem Versuch auch die erwähnte Gegenüberstellung von Wärme und Kälte erläutert werden. Sobald die gleiche Menge des gleichen Stoffes an einer Stelle des Kreislaufes Wärme aufnimmt, muss an einer anderen Stelle die gleiche Menge Wärme abgegeben werden. In diesem Fall an den zwei Wasserbehältern mit je 1 kg Inhalt. Dann, und nur dann, gilt die Aussage, dass das Abführen von Wärme (das Abkühlen), die Aufnahme von Wärme im gleichen Maße an einer anderen Stelle zur Folge hat.
Sicherheitshinweise
Beim Betrieb der Wärmepumpe ist darauf zu achten, dass der Druck nicht über 15 bar steigt. Es gibt allerdings einen Überdruckschutzschalter, der das Modell im Falle eines zu hohen Druckes abschaltet. Es ist daher unbedingt notwendig, die Gefäße mit Wasser zu befüllen und Verdampfer und Verflüssiger darin zu tauchen. Anderenfalls steigt der Druck sehr schnell an. <br\> <br\> Des weiteren sollte darauf geachtet werden, die Metallrohre während des Betriebs und auch anschließend nicht zu berühren, da dies zu Verbrennungen oder Verkühlungen führen kann.
Literatur
- ↑ Kircher, E.; Schneider, W. B. (2002): Physikdidaktik in der Praxis; Springer Verlag, Berlin, Heidelberg, New York
- ↑ Müller, R.; Wodzinski, R.; Hopf, M. (2011): Schülervorstellungen in der Physik; Aulis Verlag
- ↑ Tetrafluorethan als Kältemittel [09.03.2015]
- ↑ Spezifische Wärmekapazität von Wasser [09.03.2015]
- ↑ Checkliste Wärmepumpen, S.2 [17.03.2015]