Bestimmung der Federkonstante mittels Kraftmesser
| Bestimmung der Federkonstante mittels Kraftmesser | |
 Für die Experimente wurde das Cobra4 Mobile-Link Basis-Set Physik benutzt. | |
| Kurzbeschreibung | |
|---|---|
| In diesem Wiki-Artikel werden zwei Varianten vorgestellt, um die Federkonstante einer Feder zu bestimmt. Der didaktische Schwerpunkt liegt dabei auf den Messunsicherheiten. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 10 |
| Basiskonzept: | System |
| Sonstiges | |
| Durchführungsform | Demoexperiment oder Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 2 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Viola Schmidt |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Dr. Franz Boczianowski |
In diesem Artikel werden zwei Experimente vorgestellt, bei denen mit Hilfe eines digitalen Kraftmessers die Federkonstante einer Feder bestimmt werden kann. Dies ist zum Einen über die Bestimmung der Periodendauer in Abhängigkeit zur angehängten Masse und zum Anderen über die Auslenkung der Feder in Abhängigkeit zur Kraft möglich. Die Versuche geben die Möglichkeit, sich mit dem Thema Messunsicherheiten und dem Vertrauen zu Messergebnissen auseinander zu setzen.
Inhaltsverzeichnis
Didaktischer Teil
Zu den Aufgaben des Physikunterrichts gehört es, sich mit der „Natur der Naturwissenschaften“ zu beschäftigen (vgl. Kircher, Girwidz, Häußler (Hrsg.)[1] (2007), S. 34). Dazu muss auch ein Verständnis entwickelt werden, wie Messergebnisse zu interpretieren sind. Messunsicherheiten spielen dabei eine wichtige Rolle. Ein einfaches Alltagsbeispiel hilft das zu veranschaulichen: Ich möchte mein Zimmer neu einrichten und habe gemessen, dass meine Wand 3,1m lang ist. Der Schrank, der nach Angabe 3,00m lang ist, müsste also passen. Ich habe aber mit einem Zollstock gemessen und musste ihn mehrmals neu anlegen, wodurch jedes Mal eine Unsicherheit entsteht. Mit dieser Information weiß ich nun, dass es besser ist, nicht den Schrank zu kaufen, der genau 3,00m ist, da er eventuell nicht passen könnte. In anderen Bereichen wie der Luft- und Schifffahrt können Kenntnisse der Unsicherheit sogar Lebenswichtig sein.
Auch für die Erkenntnisgewinnung spielen die Unsicherheiten eine große Rolle. Vergleicht man die Theorie mit den experimentellen Messwerten, so muss man wissen, ob Abweichungen von der Theorie mit den Messunsicherheiten erklärt werden können oder ob eine neue Theorie entwickelt werden muss. Zusätzlich werden häufig Messergebnisse verglichen, die man über verschiedene Verfahren gewonnen hat (vgl. Kircher, Girwidz, Häußler (Hrsg.)[1] (2007), S. 35). Werden Messunsicherheiten nicht thematisiert, so könnte sich bei den Schülerinnen und Schülern die Fehlvorstellung bilden, dass sich durch einmaliges Messen der wahre Wert einer Messgröße bestimmen lässt und eine physikalische Theorie bestätigt oder verworfen werden kann (vgl. Hellwig [2](2012) S. 7).
Die hier beschriebenen Versuche bieten Anlass sich über Messunsicherheiten Gedanken zu machen. Dazu könnten zum Beispiel in einer Gruppenarbeit auf verschiedene Weise die Federkonstanten von Federn bestimmt werden, die nach Angaben des Herstellers die gleiche Federkonstante haben müssten. Eine weitere Methode zur Bestimmung der Federkonstante ist hier beschrieben. Die Gruppen werden dabei nicht alle den gleichen Wert erreichen. Dies kann erst durch Betrachtung der Unsicherheiten erklärt werden.
Die Auswertung der hier beschriebenen Versuche wurde auf universitären Niveau vorgenommen. In der Schule ist es sinnvoll eine didaktische Reduktion bei der Fortpflanzung von Messunsicherheiten vorzunehmen. Eine Möglichkeit ist dabei die absoluten Unsicherheiten bei Summen und Differenzen zu addieren und bei Produkten und Quotienten die relativen Unsicherheiten zu addieren. Eine weitere Möglichkeit ist es, einen minimalen und einen maximalen Wert zu berechnen, indem jeweils die obere oder untere Grenze des Fehlerintervalls zum Messwert eingesetzt wird. Gut beschrieben sind die Verfahren unter Fehlerrechnung leicht gemacht.
Versuchsanleitung
Aufbau
Bestimmung der Periodendauer in Abhängigkeit zur Masse
Materialien:
- aus Cobra4 Mobile-Link Basis-Set Physik inkl. Software (Artikel-Nr.: 15601-88): Cobra4 Mobile Link, Cobra4 Sensor-Unit Force
- PC (mit Software measure Cobra4)
- Feder
- Stativmaterial
- Gewichte (100g - 600g)
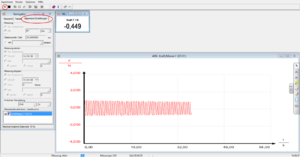
Der Aufbau ist in Abbildung 1 dargestellt. Der Mobile Link kann einfach mit der Sensor-Unit Force zusammengesteckt werden. Die Sensor Unit Force hat eine Schraubung, an die eine Stativstange angebracht werden kann. Das Messgerät kann so mit Hilfe einer Tischklemme am Tischrand befestigt werden. Des Weiteren muss an die Sensor-Unit Force der Haken angebracht werden, an dem nun eine Feder gehängt werden kann. Es wird ein PC mit der Software measure Cobra4 benötigt. Hier muss der USB-Stick eingesteckt und das Programm geöffnet werden. Schaltet man nun den Mobile Link ein, werden die Daten über W-Lan übertragen und das Programm erkennt das Messgerät automatisch. Die zeitlich eAuflösung lässt sich einstellen, wie in Abbildung 3 zu sehen ist. Für dieses Experiment sollte die genaueste Auflösung von 16 Hz gewählt werden.
Bestimmung der Auslenkung in Abhängigkeit zur Kraft
Materialien:
- aus Cobra4 Mobile-Link Basis-Set Physik inkl. Software (Artikel-Nr.: 15601-88): Cobra4 Mobile Link, Cobra4 Sensor-Unit Force
- PC (mit Software measure Cobra4)
- Feder
- Stativmaterial
- Gewichte (100g - 600g)
- Lineal mit Ständer
Die Einrichtung der Messgeräte ist identisch zum oben beschriebenem Experiment. Der Aufbau unterscheidet sich nur so weit, dass die Feder am besten an einem Stativ oberhalb des Tisches angebracht wird. So kann auf dem Tisch das Lineal im Ständer stehen, sodass die Position der Feder bestimmt werden kann. Der Aufbau ist in Abbildung 2 zu sehen.
Durchführung
Bestimmung der Periodendauer in Abhängigkeit zur Masse
Zunächst werden 100g an die Feder gehängt. Die Feder wird nun ausgelenkt und in Schwingung gesetzt. Dabei ist darauf zu achten, dass die Feder nur nach oben und unten schwinkt und keine Schwingungen in anderen Richtungen auftreten. Die Messung kann nun, wie in Abbildung 3 dargestellt ist, gestartet werden. Am PC ist nun eine sinusförmige Schwingung zu sehen. Die Tiefpunkte ergeben sich, wenn die Feder am meisten gestaucht ist. Hier wirkt die geringste Kraft auf den Kraftmesser. Bei größter Streckung der Feder ergeben sich Hochpunkte in dem Diagramm. Nach dem Stoppen der Messung wird man automatisch gefragt, ob die Messwerte dem Auswertungsprogramm übergeben werden sollen. Hier können sie abgespeichert werden. Genauso wird nun in hunderter Schritten bis zu 600g weiter verfahren.
Bestimmung der Auslenkung in Abhängigkeit zur Kraft
Zunächst wird die Position der Feder ohne angehängtes Gewicht bestimmt. Das Messgerät der Kraft muss auf Null gesetzt werden, sodass das Gewicht der Feder nicht mit eingeht. Nun wird zunächst 100g angehängt. Es muss etwas gewartet werden, bis die Feder sich wieder in Ruhe befindet. Die neue Position der Feder kann dann bestimmt werden. Aus der Differenz ergibt sich die Auslenkung. Die Kraft, die auf die Feder wirkt, kann am Messgerät direkt abgelesen werden. So wird weiter verfahren bis zu 600g.
Ergebnisse
Bestimmung der Periodendauer in Abhängigkeit zur Masse
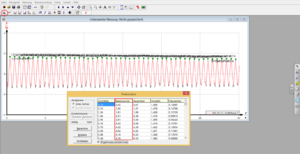
Mit Hilfe des Programms measure Cobra4 lassen sich die Hochpunkte bestimmen, was in Abbildung 4 gezeigt wird. Die Punkte können nun zu einem Tabellenkalkulationsprogramm übergeben werden. Die Periodendauer T ergibt sich durch die Differenz von zwei aufeinanderfolgenden Hochpunkten. Aus den Werten für die Periodendauer T kann ein Mittelwert gebildet werden, sowie die Standartabweichung s bestimmt werden. Für die Messunsicherheit entscheidend ist hierbei die zeitliche Auflösung des Messgerätes. Diese Beträgt 0,06s. Da der Wert der Periodendauer T durch eine Differenz gebildet wird, ergibt sich die Unsicherheit des Messgerätes durch:
Der Gesamtfehler ergibt sich aus der pythagoreischen Addition des Messgerätefehlers und der Standartabweichung s.
In der Tabelle sind die berechneten Mittelwerte mit dem Gesamtfehler angegeben. Die Fehler der Masse m sind dem Skript zum physikalischen Grundpraktikum S. 18 [3] entnommen.
| Masse m [kg] | Periodendauer T [m] |
|---|---|
Bestimmung der Auslenkung in Abhängigkeit zur Kraft
Die Ergebnisse sind der Tabelle zu entnehmen. Die Unsicherheit für die Kraft F beträgt 0,05N und ist der Betriebsanleitung [4] entnommen. Die Unsicherheit des Maßstabes ist dem Skript zum Grundpraktikum S. 17 [5] entnommen. Er beträgt:
Diese Unsicherheit ist allerdings so klein, dass sie gegenüber der Unsicherheit beim Ablesen vernachlässigt werden kann. Der Ablesefehler wird auf 1mm abgeschätzt, da die Feder beweglich ist. Da die Auslenkung l aus der Differenz berechnet wird, ergibt sich die Unsicherheit wieder durch:
| Kraft F [N] | Auslenkung l [m] |
|---|---|
Auswertung
Bestimmung der Periodendauer in Abhängigkeit zur Masse
Für die Periodendauer eines Federpendels gilt:
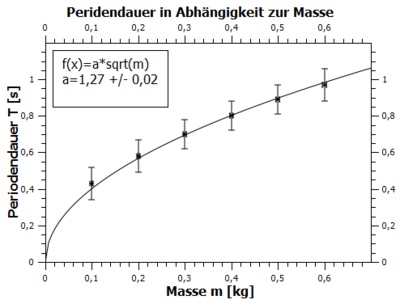
Die Werte für die Periodendauer T in Abhängigkeit zur Masse m wurden in QTI-Plot geplottet und mit Hilfe der Funktion mit gefittet. Der Fit ist in Abbildung 5 zu sehen. Für a ergibt sich dabei . Aus dem Faktor a lässt sich nun die Federkonstante D bestimmen:
Die Unsicherheit ergibt sich durch:
Damit ergibt sich
Bestimmung der Auslenkung in Abhängigkeit zur Kraft
Mit Hilfe der Formel
lassen sich mit den Messwerten, die Tabelle 2 zu entnehmen sind, jeweils die Federkonstante D bestimmen. Aus den 6 Werten wurde ein Mittelwert gebildet und die Standardabweichung bestimmt. Die Standartabweichung beträgt . Zusätzlich muss noch die Unsicherheit der Messgeräte mit berücksichtigt werden:
Diese Unsicherheit ist gegenüber der Standardabweichung klein und so ergibt sich insgesamt mit Hilfe dieser Methode . Die beiden Werte, die für die Federkonstante D mittels zwei verschiedener Methoden bestimmt wurden, überlappen sich damit in ihrem Fehlerintervall.
Literatur
- ↑ 1,0 1,1 Kircher E./ Girwidz R./ (Hrsg.) (2007): Physikdidaktik. Theorie und Praxis; Springer-Verlag, Berlin Heidelberg, 2. Auflage 2009
- ↑ Hellwig J.: Messunsicherheiten verstehen- Entwicklung eines normativen Sachstrukturmodels am Beispiel des Unterrichtsfaches Physik; Ruhr-Universität Bochum 2012, verfügbar unter Dissertation
- ↑ Physikalisches Grundpraktikum - Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik (2007), verfügbar unter Skript [20.09.2016]
- ↑ Betriebsanleitung Phywe Cobra4 Sensor-Unit Kraft ±40 N, verfügbar unter Betriebsanleitung [20.09.2016]
- ↑ Physikalisches Grundpraktikum - Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik (2007), verfügbar unter Skript [20.09.2016]