Bestimmung der Erdbeschleunigung mit dem Kugelfallgerät

Bestimmung der Erdbeschleunigung mit dem Kugelfallgerät
Kugelfallgerät mit Digitalzähler
Kurzbeschreibung
Qualitative bestimmung der Erdbeschleunigung über den Freien Fall
Kategorien
Mechanik
Einordnung in den Lehrplan
Geeignet für:	Klasse 9
Basiskonzept:	Wechselwirkung
Sonstiges
Durchführungsform	Schüler*innen-Experiment
Anzahl Experimente in dieser Unterkategorie	1
Anspruch des Aufbaus	leicht
Informationen
Name:	Esra Demir
Kontakt:	${\text{demiresx}}$@${\text{cms.hu-berlin.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Johannes Schulz

Der freie Fall wird in der neunten Klasse unter dem Bereich „Schneller werden und Bremsen“ eingeführt.
Als Beispiel einer gleichmäßig beschleunigten Bewegung wird in diesem Versuch der freie Fall einer Kugel untersucht.
Mithilfe eines Weg-Zeit-Diagrammes, kann man die Erdbeschleunigung bestimmen.

Didaktischer Teil

Das Kugelfallgerät ist ein sehr abstraktes Gerät, das im Alltag so nicht existiert.
Daher kann man beispielsweise mit einem Schülergruppenexperiment anfangen, wie von Sarah Heydemann Freier Fall mit der Fallschnur beschrieben und danach auf das Kugelfallgerät übergehen. Mit der Fallschnur zu beginnen ist gut, weil die Schüler selbst die Muttern in der richtigen Reihenfolge anbinden müssen und am Ende beschreiben können, was sie sehen beziehungsweise was sie hören. Die Fallschnur ist ein induktives Experiment, das heißt durch Experimente entwickelt man gemeinsam mit den Schülern und Schülerinnen die Theorie die dazu gelehrt werden soll. Das Kugelfallgerät dagegen ist ein deduktives Experiment, man Lehrt die Theorie und anschließend folgt der Versuch.
Der Vorteil ist, dass man beim induktiven Experiment nie zu weit von der Experimentalphysik ist, jedoch haben die deduktiven Experimente den Vorteil, dass Bereiche in der Physik zugänglich werden, die alleine mit Experimenten nicht zugänglich sind. Daher ist die Kombination von Fallschnur und im Anschluss Kugelfallgerät sehr sinnvoll, denn nur deduktives ist ein dorniger Weg. Eine Unterrichtseinheit der teils Induktiv und teils Deduktiv ist, stellen die beiden genannten Versuche da.[2]
Dadurch vertieft sich das Thema des Freien Falls und dieses Wissen kann man bei jedem Versuch des freien Falls wieder aufgreifen. Das Wissen von dem hier gesprochen wird, wird von Sarah Heydemann Freier Fall mit der Fallschnur sehr gut beschrieben. Das Kugelfallgerät ist abstrakter, weil die Schüler und Schülerinnen sich mehr mit dem dem mathematischen Teil befassen müssen, das heißt, Tabellen aufstellen, Formel umstellen und Diagramm erstellen. Bei dem Kugelfallgerät erkennen Schüler und Schülerinnen, was sie schon Wissen, dass bei längerer Strecke mehr Zeit benötigt wird.
Bei beiden Versuchen wirkt die Erdbeschleunigung mit ein, daher kann man dieses eher bei beiden Versuchen experimentell bestimmen. Bei der Fallschnur wird es mithilfe einer Audio Aufnahme bestimmt und bei dem Kugelfallgerät wird es anhand des s-t-Diagrammes bestimmt.

Wichtig ist auch das man die Messunsicherheit hier in Betracht zieht.
Mit Messunsicherheiten sollte man früh anfangen zu arbeiten, da sie ein sehr großes Problem bei Schüler und Schülerinnen ist.
Es wird dadurch beim Berechnen der Messunsicherheit, nach dem alle Messwerte aufgenommen wurden, bei dem Versuch ein Wertebereich eingeschränkt, in dem der wahre Wert des Versuches liegt.
Beim Kugelfallgerät ist es vor allem sehr sinnvoll die Messunsicherheiten einzubeziehen, da das Gerät sehr präzise in der Messung ist. Bei der Fallschnur dagegen ist die Messung nicht so genau wie mit dem Kugelfallgerät. Man muss bei dem Versuch darauf achten, dass die Tonaufnahme ab dem ersten Klicken genau gemessen wird und man hat Nebengeräusch, die das einzelne erfassen des Geräusches erschweren.
Durch den Digitalzähler, der den Start der Kugel und den Stopp der Kugel direkt aufnimmt ist die Unsicherheit sehr gering, denn dieser zeigt die Sekunde bis zu einem 1000tel genau an. Wichtig ist, dass man zu einem 10tel genau Messdaten aufnehmen kann und diese nahe am Literaturwert 9,81 m/s² liegen.[3]
Das Thema der Messunsicherheiten kann nie früh genug eingeführt werden, daher sollte mit den Experimente das Verständnis für die Messunsicherheiten etwas verbessert werden.
Daher kann mit den verschiedenen Versuchen zum freien Fall viele Missverständnisse bei der Messunsicherheit aufheben, da der Wert den man berechnet hat in einem gewissen Wertebereich liegt und man nicht einen zu großen Fehler kriegen sollte und man erkennt wie gut die eigene Berechnung der Erdbeschleunigung bei dem Kugelfallgerät ist.

Versuchsanleitung

Aufbau

Material:

• Kugelfallgerät bestehend aus:

1. Auslöser für die Kugel
2. Fangschalter
3. 1 Meter Lineal

• Digitalzähler
• Vier Verbindungskabel
• Stahlkugel

Der Versuch ist ein leichter Aufbau. Wenn man das Kugelfallgerät nicht als ein ganzes Gerät hat, wie in diesem Artikel, kann man dieses auch nachbauen mit einer Stativstange und einem Stativfuß, sowie ein Auslöser und einem Fangschalte, die man mit Doppelmuffen anbringen kann.

Durchführung

Für die Durchführung wird das Kugelfallgerät wie in der oberen Abbildung aufgebaut. Die Auslöserplatte und der Fangschalter werden durch die Verbindungskabel mit dem Digitalzähler verbunden. Dieser Digitalzähler misst die Fallzeit (s) in Sekunden. Der Versuch wird mehrmals durchgeführt in verschiedenen Höhen, diese werden dann notiert. Die Auslöserplatte wird in 0,5 cm Schritten in der Höhe verändert, die man anhand des Lineals ablesen kann. An dem Auslöser ist ein Magnet, der die Kugel anzieht. Stellt man diesen Auslöser mit der Kugel in einer bestimmten Höhe ein, wird der Startschalter an dem Auslöser betätigt, dabei wird die Fallzeit von dem Digitalzähler gemessen. Die gemessene Zeit wird unterbrochen, sobald die Kugel das erste Mal den Fangschalter berührt. Die gemessene Zeit wird notiert. Am Ende des Versuches werden die Fallzeiten quadriert und dann in einer Grafik mit Fallstrecke über Fallzeit zum Quadrat aufgetragen.

Ergebnisse

Als Ergebnis erhält man, dass die Fallstrecke (s) zu der Fallzeit (t) keine lineare Funktion ist, sondern parabelförmig. Dagegen ist die Fallstrecke proportional zum Quadrat der Fallzeit, wenn man das in eine Grafik überträgt ergibt es eine lineare Funktion.

Auswertung

Es werden verschiedene Höhen und Zeiten notiert, die Fallzeite werden dann quadriert. Die Messungen wurden in 0,5 cm Schritten durchgeführt, daraus ergab sich die folgende Tabelle:

Tabelle 1: Messwerte

s in m	t in s	t² in s²
0,05	0,102	0,010
0,10	0,143	0,020
0,15	0,176	0,031
0,20	0,201	0,040
0,25	0,226	0,051
0,30	0,248	0,062
0,35	0,261	0,068
0,40	0,286	0,082
0,45	0,302	0,091
0,50	0,319	0,102
0,55	0,334	0,112
0,60	0,349	0,122
0,65	0,364	0,132
0,70	0,377	0,142
0,75	0,390	0,152
0,80	0,404	0,163
0,85	0,415	0,172
0,90	0,428	0,183
0,95	0,439	0,193
1,00	0,446	0,199

Die Messunsicherheiten von t uns s wurden abgeschätzt, es ergab sich für die Unsicherheit von s: u_s = 0,01 m und für die Unsicherheit von t: u_t = 0,05 s.

Je Länger die Fallstrecke ist, desto mehr Zeit wird benötigt.

Da es sich um einen qualitativen Versuch handelt, bei dem die Erdbeschleunigung (g) bestimmt werden soll, nutzen wir die obere Tabelle um eine Grafik mit s über t und s über t² zu erstellen.

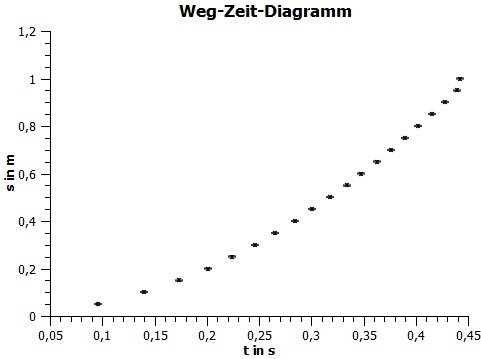
Garfik 1: Weg-Zeit-Diagramm (s über t):

Wenn man s über t aufträgt erhält man eine Parabolische Funktion.

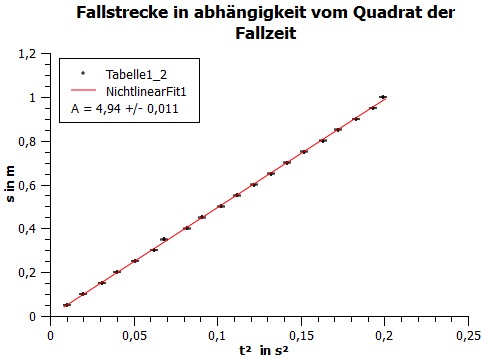
Grafik 2: Fallstrecke in Abhängigkeit vom Quadrat der Fallzeit:

Im Gegensatz zur Grafik 1 ist diese Grafik eine linear Funktion, damit lässt sich sagen, dass die Fallstrecke proportional zum Quadrat der Fallzeit ist. Die obigen Grafiken wurden mit dem Programm Qtiplot erstellt. Dabei wurde eine Steigung berechnet die wie in Grafik 2 lautet: a = 4,94 ± 0,01.

Berechnung von der Erdbeschleunigung

Im Allgemeinen ist die Formel für den freien Fall s = 1/2gt². Formt man diese Formel um nach g erhält man: g = 2s/t². Da unsere Steigung anhand der Formel a = s/t² berechnet wurde, ergibt sich in diesem Falle für g = 2a. Die Messunsicherheit von g wurde mithilfe der Gausß'schen Fehlerfortpflanzung berechnet, die wie folgt lautet:
u_g = √((2/t²) u_s)² + (((-4s)/t³) u_t)².

Es ergab sich für die Erbeschleunigung folgender Wert: g =(9,88 ± 0,02) m/s².

Literatur

[1] Anleitung un Messbeispiel zum Kugelfallgerät
[2] Physikdidaktik kopakt
[3]Literaturwert

Siehe auch

1. Freier Fall mit der Fallschnur [[4]]
2. Messung der Erdbeschleunigung mittels Fotografie [[5]]