Bestimmung der Elementarladung mithilfe des Millikan-Versuches
| Bestimmung der Elementarladung mithilfe des Millikan-Versuches | |
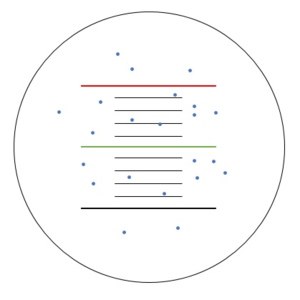
 Aufbau des Millikan-Versuches zur Messung der Elementarladung | |
| Kurzbeschreibung | |
|---|---|
| Messung der Elementarladung durch Überlagerung mehrerer Kräfte innerhalb zweier Kondensatorplatten | |
| Kategorien | |
| Atom- und Kernphysik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung, Materie |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | David Winderlich |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Der Millikan-Versuch ist nach dem amerikanischen Physiker Robert Andrew Millikan benannt, dem es mithilfe dieses Experiments 1910 gelang, die Elementarladung sehr genau zu bestimmen. Der Kern des Millikan-Versuches besteht aus einer Überlagerung von Kräften, welche auf ein Öltröpfchen wirken. Mathematische Umformungen erlauben es bei Kenntnis der Kraftansätze auf die Größe der Elementarladung zu schließen. Es Versuch kann auf mehrere Arten durchgeführt werden, die sich in ihrer Komplexität unterscheiden.
Inhaltsverzeichnis
Didaktik
Es soll hier um die Bedeutung des Experiments gehen, sowohl aus historischer Sicht, als auch um die Bedeutung in der Schule.
Historisch betrachtet ist der Millikan-Versuch wohl einer der bedeutendsten Versuche der Physik, liegt ihn ihm doch die Grundlage zur Entdeckung der Quantelung der elektrischen Ladung. Für die Schule bildet er den einzigen Versuch, in dem der Nachweiß über die Quantelung der Ladung und die Bestimmung der Elementarladung direkt möglich ist. Da diese Erkenntnis wesentlich für die Quantenphysik ist, ist der Versuch wichtiger Bestandteil des Physikunterrichts. Schon vor dem Millikan-Versuch gab es Hinweise darauf, dass es eine feste Elementarladung gibt. So war durch chemische Versuche bekannt, dass man für die Elektrolyse einer Stoffmenge immer den selben Strom benötigt. Jedoch ließe sich das auch dadurch erklären, dass dies durch den Mittelwert von nicht exakt gleich geladenen Teilchen zustande kommt. Erst der Millikan-Versuch ermöglichte eine exakte Bestimmung des Wertes. Die Suche nach der Elementarladung war um die Zeit um 1900 eines der vordringlichsten Probleme der Physik.[1] Die Entdeckung half Nils Bohr beim Entwickeln seines Atommodells, welches die Atomphysik vorantrieb. Darüber hinaus konnte man durch Elektronenbewegungen im Magnetfeld nun auch auf die Masse von Elektronen schließen.
Im Unterricht bietet das Experiment ein hohes didaktisches Potenzial durch:[2]
- Entwicklung einer Messmethode zur Ladungsbestimmung
- Gewinnung, Darstellung und Auswertung größerer Datenmengen
- Geschichtliches zum Versuch, wie Hypothesen zur Existenz der Ladungsquantelung, der historische Versuchsaufbau und Details der Versuchsdurchführung, die Durchführung der Originalmessungen und Millikan als Wissenschaftler Hier wäre auch eine Auseinandersetzung mit den Kritiken zum Versuch angebracht. So hat der Physiker Felix Ehrenhaft bei ähnlichen Messungen streuende Werte erhalten. Der Wissenschaftshistoriker Gerald Holton stellte fest, dass Millikan die Ergebisse seiner Messungen geschönt hatte um die Vorwürfe von Ehrenhaft zu entkräften.[3]
Ausßerdem lassen sich anhand des Millikan-Versuch mehrere physikalische Konzepte behandeln, z.B. die Bewegung geladener Teilchen in elektrischen Feldern, sowie Überlagerung von Kräften.
Versuchsanleitung
Der Millikan-Versuch kann auf bis zu 4 verschiedene Arten durchgeführt werden. Diese unterscheiden sich weniger im Aufbau, als viel mehr im Ablauf des Versuches. Dadurch fallen die Kraftansätze unterschiedlich aus, was eine unterschiedliche Komplexität der Umformungen zur Folge hat. Allen Versuchen gemein sind die Öltröpfchen, die sich innerhalb eines horizontalen Plattenkondensators befinden, auf die die Gewichtskraft wirkt. In diesem Versuch wird die Schwebe-Sink-Methode behandelt, bei der ein Öltröpfchen zuerst im elektrischen Feld nach oben steigt und danach bei ausgeschaltetem elektrischen Feld nach unten fällt.
Geräte
- Millikan-Gerät
- Netzgerät mir regelbarer Gleichspannungspannung 0-400V
- Netzgerät mit einer Spannung von 12V
- Voltmeter zum Ablesen der angelegten Spannung
- 2 Stoppuhren (normale Handstoppuhren oder autom. funktionierende, welche in den Stromkreis einfließen)
- Videokamera welche das Bild an einem Projektor/Fernseher ausgibt.
- Wasserwaage
Aufbau
Die Kondensatorplatten am Millikan-Gerät werden mit dem Netzgerät(0-400V) so verbunden, dass an der oberen Kondensatorplatte Plus anliegt, an der unteren Minus. Dazu parallel wird das Voltmeter geschalten. Die Kondensatorplatten sollten mithilfe einer Wasserwaage parallel zum Erdboden ausgerichtet werden. Das Netzgerät mit einer Spannung von 12V wird an die Leuchtquelle angeschlossen, welche sich ebenfalls am Millikan-Gerät befindet. Vor das Mikroskop des Millikan-Geräts wird die Kamera so positioniert, dass nach Scharfstellen der Kamera, sowie des Mikroskops das innere der Kondensatorkammer gut zu sehen ist. Das Bild kann vermutlich erst während dem Versuch richtig eingestellt werden. Benutzt man Stoppuhren, welche automatisch beim Einschalten/Umpolen des Plattenkondensators starten/stoppen, so muss man diese entsprechend der Bebilderung auf dem Gerät an das Netzgerät anschließen. Handstoppuhren funktionieren jedoch ebenso gut, nur, dass diese selbstständig betätigt werden müssen. Diese Arbeit kann an Schülerinnen und Schüler übergeben werden.
Beteiligte Kräfte und Größen
- die Gewichtskraft mit , wobei die Masse des Tröpfchen und die Erdbeschleunigung ist.
- die elektrische Kraft mit , wobei die Ladung, die angelegte Spannung und der Abstand der Kondensatorplatten ist. Den Abstand entimmt man aus der Bedienungsanleitung des Millikan-Gerätes. In diesem Versuch betrug der Abstand 6mm.
- die Stokessche Reibungskraft mit , wobei die Viskosität, der Radius des Tröpfchen und dessen Geschwindigkeit ist.
- die Dichte der Öltröpfchen
- die Viskosität der Luft
- der Abstand zweier Skalenteile am Mikroskop entsprechen
Ansatz und Umformung
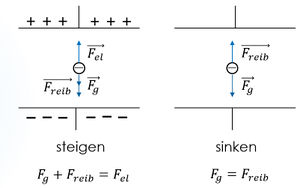
Beim steigenden Öltröpfchen herrscht folgendes Kräftegleichgewicht (siehe Skizze)
und damit
Beim sinkenden Öltröpfchen gilt hingegen folgendes Kräftegleichgewicht
und damit
Auch hier wird die Masse wieder ersetzt mit .
Durch Umstellen der zweiten Gleichung nach und Einsetzen in die erste Gleichung erhält man schließlich
Bis auf die zu messenden Größen der Geschwindigkeiten und der Spannung ist alles bekannt.
Versuchsdurchführung
Vor dem Versuch muss sich darauf geeinigt werden, welche 2 Linien man als Start- bzw. Zielpunkt man für die Zeitmessung nimmt. In diesem Beispiel sind diese in der Skizze rot bzw. grün hervorgehoben.
- Schritt: Bevor der Plattenkondensator eingeschaltet wird, wird bereits vorher eine Spannung eingestellt und protokolliert. Während dem Versuch soll nicht an der Spannung gedreht werden.
- Schritt: Einsprühen der Öltröpfchen durch kräftiges Drücken der Pumpe. Falls noch nicht geschehen, Einstellen der richtigen Schärfe der Kamera und des Mikroskops.
- Schritt: Die Tröpfchen fallen nach unten, da kein elektrisches Feld vorhanden ist. Es wird ein Tröpfchen herausgesucht, welches beobachtet werden soll und sich unterhalb der grünen Linie befindet.
- Schritt: Einschalten des Plattenkondensators. Das beobachtete Tröpfchen sollte sich nach oben bewegen. Bewegt es sich weiter nach unten, so muss der Plattenkondensator wieder ausgeschaltet werden und man wiederholt das Ganze.
- Schritt: Sobald das nach oben bewegende Tröpfchen die grüne Linie berührt, wird die erste Zeitmessung gestartet.
- Schritt: Ist das Tröpfchen an der roten Linie angekommen, wird gleichzeitig der Plattenkondensator ausgeschaltet, die erste Zeitmessung gestoppt und die zweite Zeitmessung begonnen.
- Schritt: Das Tröpfchen bewegt sich nun wieder nach unten. Berührt es wieder die grüne Linie, wird auch die zweite Zeitmessung gestoppt. Beide Zeiten werden protokolliert. Da der Abstand zwischen den Linien aus der Bedienungsanleitung bekannt ist, können die Geschwindigkeiten einfach mit berechnet werden.
- Schritt: Gemessene Werte für die Spannung und der Zeit werden in die Gleichung eingesetzt. Das Ergebnis ist ein Vielfaches der Elementarladung .
Messwerte
Bei der Durchführung einer Messreihe erhielt man folgende Ergebnisse:
| # | Spannung in V | Steigzeit in s | Fallzeit in s |
|---|---|---|---|
| 1 | 200 | 5,93 | 19,87 |
| 2 | 200 | 2,9 | 16,18 |
| 3 | 200 | 5,1 | 13,26 |
| 4 | 200 | 3,61 | 34,53 |
| 5 | 200 | 3,71 | 14,02 |
| 6 | 200 | 1,09 | 7,52 |
| 7 | 200 | 1,35 | 9,06 |
| 8 | 200 | 5,57 | 6,2 |
| 9 | 200 | 9,41 | 9,2 |
| 10 | 200 | 3,9 | 16,52 |
Auswertung
Hat man die Zeiten gemessen, kann man aufgrund des bekannten Weges auf die Geschwindigkeiten schließen. Zusammen mit der gemessenen Spannung hat man alle Werte, um die oben bereits gezeigte Formel
zu lösen. ist dabei ein Vielfaches der Elementarladung. Trägt man die Werte in ein Diagramm ein, sollten sich theoretisch jeweils Ansammlungen bei Vielfachem der Elementarladung finden.
Messunsicherheiten
Natürlich ist dieses Experiment nicht frei von Unsicherheiten. Die größte Unsicherheit spielt dabei wohl der Faktor Mensch. Ein exakte Zeitmessung würde verlangen, dass man die Zeit jeweils dann nimmt, wenn das sich das beobachtete Öltröpfchen genau über den Markierungen befindet. Da die Tröpfchen aber eine gewisse Geschwindigkeit haben und die Striche eine bestimmte Dicke, ist dies nicht fehlerfrei möglich. Auch die Geräte haben einen gewissen Fehler. So ist nicht z.B. zu erwarten, dass das Spannungsversorgungsgerät exakt 200V liefert. Ebenso spielen Einflüsse wie Verdunstung eine Rolle. Jedoch fallen diese im Gegensatz zum Faktor Mensch deutlich weniger ins Gewicht und es wird ihnen demnach keine weitere Beachtung geschenkt. Für die Zeitmessung wird ein Fehler von 0,3s angesetzt. Da die Skala im Mikroskop laut Bedienungsanleitung einen Abstand von 0,00053m für 10 Skalenteile angibt, wird ein Zehntel davon als Fehler abgeschätzt. Damit ergibt sich eine Unsicherheit bei der Geschwindigkeit, welche eine Unsicherheit bei der Ladung nach sich zieht. Die Werte für die Unsicherheiten wurde mithilfe der Gaußschen Fehlerfortpflanzung berechnet.
Ergebnisse
Unter Einbezug der Unsicherheiten berechnete Ergebnisse:
| # | Geschw. steigend in | Geschw. fallend in | Unsicherheit der Geschw. steigend in | Unsicherheit der Geschw. fallend in | Ladung in | Unsicherheit der Ladung in |
|---|---|---|---|---|---|---|
| 1 | 1,79 | 0,53 | 0,13 | 0,03 | 1,69 | 0,09 |
| 2 | 3,66 | 0,66 | 0,42 | 0,03 | 3,48 | 0,34 |
| 3 | 2,08 | 0,80 | 0,16 | 0,04 | 2,57 | 0,14 |
| 4 | 2,94 | 0,31 | 0,28 | 0,02 | 1,79 | 0,16 |
| 5 | 2,86 | 0,76 | 0,27 | 0,04 | 3,13 | 0,24 |
| 6 | 9,72 | 1,41 | 2,72 | 0,09 | 13,19 | 3,22 |
| 7 | 7,85 | 1,17 | 1,79 | 0,07 | 9,73 | 1,93 |
| 8 | 1,90 | 1,71 | 0,14 | 0,19 | 4,71 | 0,18 |
| 9 | 1,13 | 1,15 | 0,67 | 0,07 | 2,44 | 0,07 |
| 10 | 2,72 | 0,64 | 0,25 | 0,03 | 2,68 | 0,20 |
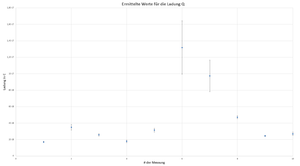
Die Werte für die Ladung werden in ein Diagramm eingetragen.
Hat man genug Messungen, sollten sich Häufungen von Ereignissen auf horizontalen Linien finden, dessen Ladungen Vielfache der Elementarladung entsprechen. Der Abstand zwischen 2 aufeinanderfolgenden Linien ist der Betrag der gesuchten Elementarladung .
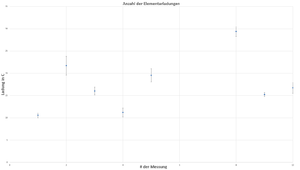
Das dies mit diesen Experiment aber nicht zu realisieren ist, soll das nächste Diagramm verdeutlichen. Hier wird der Wert der Elementarladung als bekannt vorausgesetzt. Teilt man die berechnete Ladung durch diesen Wert, sollte ein ganzzahliges Vielfaches der Elementarladung das Ergebnis sein ().
Es sei angemerkt, dass in dem zweitem Diagramm die Messungen 6 und 7 entfernt wurden. Sie waren deutlich höher als die Restlichen. Das macht sie nicht falsch/unbrauchbar, allerdings würden sie die Achse verzerren, wodurch sich die Werte schlechter Vergleichen lassen. Die Entscheidung ist der Übersichtlichkeit geschuldet.
Man kann erkennen, dass die Unischerheiten zu groß sind, um eine Aussage zur Elementarladung treffen zu können. die Ladung der Messung 2 beispielsweise schwankt ungefähr zwischen 19 und 24 Vielfachen. Messung 2 kann man also keiner der theoretisch auftretenden Häufungslinien zuordnen. Sie könnte zur 19, jedoch genauso wahrscheinlich der 24 Linie zugeordnet werden. Dieses Problem hat jeder Messwert. Ein Fehler, welcher größer als ist, ist für die Auswertung daher nutzlos. Der Aufwand dieser 10 Messungen war schon zu viel für den Einsatz als Demonstrationsexperiments in der Schule. Da man deutlich mehr (mehrere Hundert) Messungen vornehmen müsste und diese durch die zu großen Unsicherheiten dann dennoch unbrauchbar wären, ist der Einsatz mit dem Ziel der Bestimmung der Elementarladung in der Schule nicht realisierbar.
Simulation als Alternative
Zum Millikan-Versuch finden sich viele Simulationen im Internet, welche im Kern nur wenig voneinander abweichen. Oft als Java-Applet anzufinden, können diese Simulationen den Realversuch zumeist komplett ersetzen.
Szenarien, in den Simulationen eine sinnvolle Lösung sind und ihre Aufgabe im weiten Sinne sind unter Anderem :[4]
- Bei Simulationen lassen sich Abhängigkeiten und Bedeutung von Einflussfaktoren unter vereinfachten Annahmen erkennen Da die Ergebnisse einer Simulationen durch ihre Programmierung, sprich dem mathematischen Modell bestimmt ist, können äußere Umweltfaktiren völlig ausgeblendet werden, die die reale Messung beeinflussen würden. So spielen beim Millikan Versuch auch Einflüsse wie Verdunstung eine Rolle, welche sich nicht ohne weiteres nachprüfen lassen. Bei der Simulation gibt es also nur den Mensch als Unsicherheitsfaktor. Da die Bedienung einer Computersimulation aber einfach gehalten ist, die ausführende Person also sehr genau "messen" kann, wird das Ergebnis annähernd dem Literaturwert entsprechen. Unterschiedliche Ergebnisse einer Messung sind daher hauptsächlich auf unterschiedliche Startbedingungen (Spannung, Anzahl der Elementarladungen auf dem Tröpfchen) zurückzuführen. Damit lassen sich die Abhängigkeiten überprüfen.
- Simulationen helfen, wenn Geräte für die Realisierung nicht praktikabel sind Bei einem realen Versuch muss darauf geachtet werden, dass die Schärfe des Mikroskops richtig eingestellt ist. Darüber hinaus müssen die Lichtverhältnisse stimmen. Wird eine Kamera vor das Mikroskop gestellt, muss diese auch umständlich ausgerichtet werden. Außerdem eignet sich nicht jede Kamera für das Abfilmen von einem Mikroskop. Diese Dinge erschweren den ohnehin schon unpraktischen Versuch nur noch weiter. Hier liegt ein großer Vorteil der Simulation. Er hat diese Nachteile nicht. Auch muss er nicht erst "aufgebaut" werden. Mit dem Start des Programms ist der Versuch einsatzbereit. Die Auswertung kann, sofern es gewünscht ist, ebenfalls vom Programm übernommen werden. So ist es möglich, direkt nach einer Messung die Anzahl der Elementarladungen anzeigen zu lassen.
- Lernende können Simulationen auf ihren eigenen Geräten auch außerhalb des Unterrichts durchführen Eine Computersimulationen ist nicht an Spezialgeräte (Millikan-Gerät) gebunden, sondern kann überall durchgeführt werden, wo ein Zugang zum Computer besteht. Ein weiterer Vorteil liegt in der Tatsache, dass bei vorhandensein mehrerer Computer jeder Schüler für sich oder in kleinen Gruppen parallel an dem Versuch gearbeitet werden kann. So können Schülerinnen und Schüler für sich interessante Aspekte direkt selbst nachprüfen und kann ihn beliebig oft wiederholen.
Da die Bestimmung der Elementarladung mithilfe des Millikan-Versuches in der Praxis nicht in der Schule umzusetzen ist, bietet es sich an, eine Simulation heranzuziehen, um den Versuch nicht ganz den Rücken zu kehren. Simulationen arbeiten auf Basis von formal-logischen Modellen. Bei der Simulation zum Millikan-Versuch verfälschen keine Umwelteinflüsse die Messung. Bei einer Simulation sollten sich Abhängigkeiten und die Bedeutung von Einflussfaktoren unter vereinfachten Annahmen erkennen lassen.> Dies ist aufgrund der gleichbleibenden Bedingungen sogar besser umzusetzten, als beim realen Experiment. Die Simulation hat noch andere Vorteile.
Literatur
- ↑ Die Bedeutung des Millikan-Experiments
- ↑ Der Millikan-Versuch als Remotely Controlled Laboratory (RCL) Ein Artikel der didaktisch-physikalischen Frühjahrstagung in Regensburg 2007
- ↑ Zankl: Nobelpreise S. 24.
- ↑ Ernst Kircher: Physikdidaktik - 3. Auflage, Springer Spektrum, 2013