Bessel-Verfahren

Bessel-Verfahren
Linsenposition 1 Linsenposition 2 Linsenpositionen zur Bildentstehung
Kurzbeschreibung
Bestimmung von Brennweiten von Sammellinsen.
Kategorien
Optik
Einordnung in den Lehrplan
Geeignet für:	Klasse 9, Klasse 10
Basiskonzept:	System, Wechselwirkung
Sonstiges
Durchführungsform	Demoexperiment, Schüler*innen-Experiment, Gruppenexperiment
Anzahl Experimente in dieser Unterkategorie	1
Anspruch des Aufbaus	leicht
Informationen
Name:	Sven Feja
Kontakt:	${\text{fejasven}}$@${\text{student.hu-berlin.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Franz Boczianowski

Das Bessel-Verfahren wurde von Friedrich Wilhelm Bessel im Jahre 1840 veröffentlicht(vgl. Bessel (2001), S. 289-294). Mit dieser Methode kann man sehr genau die Brennweite einer Sammellinse bestimmen. Man nutzt einfache geometrische Beziehungen. Wichtig dabei ist, dass der Gegenstand und der Schirm, auf den das erzeugte Bild projieziert wird, mindestens den vierfachen Abstand der Brennweite zueinander haben müssen.

Didaktischer Teil

Das Bessel-Verfahren eignet sich gut als Schülerversuch in der 9 bzw. 10 Klasse. Begriffliche Voraussetzungen für das Verfahren sollten Brennpunkt bzw. Brennweite, Strahlengänge, (Doppel-)Brechung und Brennebene an Linsen sein und die damit verbundene Bildentstehung. Hilfreich kann auch das Wiederholen der Trigonometrie sein. Falls die diese noch nicht im Mathematikunterricht besprochen wurde, könnte man eventuell einen fachübergreifenden Unterricht mit dem jeweiligen Mathematiklehrer planen. Als gute Alternative zur Methode nach der Abbildungsgleichung ${\frac {1}{f}}={\frac {1}{g}}+{\frac {1}{b}}$ kann das Bessel-Verfahren dienen, da man z.Bsp. genauere Messergebnisse erhält. Außerdem werden die Schüler/innen mit diesem Verfahren darauf aufmerksam gemacht, dass es zwei Linseneinstellungen gibt, um ein scharfes Bild auf dem Schirm zu erzeugen (ein vergrößertes und ein verkleinertes Bild). In den meisten Abbildungen, wird häufig nur eine mögliche Bildentstehung oder ein Strahlungsverlauf dargestellt. Diese Methode hilft auch beim Verständnisprozess der Bildentstehung durch Sammellinsen.

Eine Halogenlampe mit Glühwendel (Experimentierleuchte) eignet sich gut als Lichtquelle und gleichzeitig als Gegenstand G. Auf dem Schirm werden die einzelnen Windungen als Bild B gut projiziert. Man kann so Erstaunen der Schüler erzeugen und somit das Interesse für den Versuch fördern.

Das Bessel-Verfahren könnte als Einstiegsexperiment für optische Instrumente, wie z.Bsp. das Teleskop oder das Mikroskop genutzt werden. Insbesondere das Kepler-Teleskop könnte in einer der darauffolgenden Unterrichtsstunden vom Lehrer aufgebaut werden und die dazugehörigen Strahlengänge besprochen werden. Ein anschließender Besuch in einer Sternwarte wäre dann zum Einen eine gute Vertiefung und zum Anderen bietet ein solcher Exkurs eine Abwechslung zum Schulalltag. Noch geeigneter wären eine Mond- bzw. Sonnenfinsternis, falls diese im laufenden Schuljahr gerade stattfinden, zu beobachten. Desweiteren ist es eventuell hilfreich, auch das Auge als Messinstrument zu behandeln. Dadurch würde es möglich werden auf die Genderfrage einzugehen und damit ebenfalls die Mädchen für optische Instrumente zu begeistern.

Versuchsanleitung

Abbildung 1

Abblidung 2

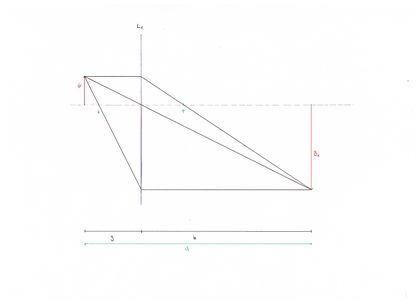
Für die Abbildung 1 und 2 gilt Abbildungsgleichung: ${\frac {1}{f}}={\frac {1}{g}}+{\frac {1}{b}}$

Die Bezeichnungen für achsennahe Strahlen sind

• f = Brennweite
• g = Gegenstandsweite
• b = Bildweite

Der Abstand d ist die Entfernung vom Gegenstand (z.Bsp. Glühbirne) zum Bild (z.Bsp. Schirm, nach g aufgelöst folgt:

${\begin{matrix}d&=&g+b&\rightarrow &g&=&d-b&&&{\text{(1)}}\\\end{matrix}}$

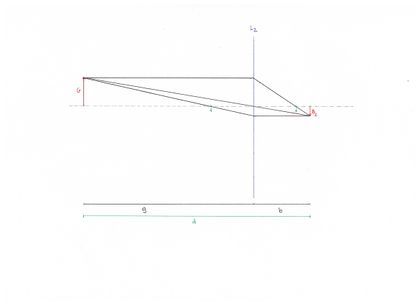
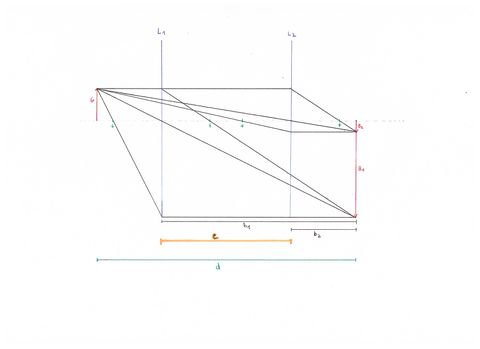
Bessel nutzte in seinem Verfahren aus, dass zwei Lösungen und damit zwei Linseneinstellungen zur Bildkonstruktion existieren. Es gibt somit zwei Bildweiten (und dadurch auch zwei Gegenstandsweiten), um ein scharfes Bild auf dem Schirm zu erhalten. Die Differenz der beiden Linseneinstellungen bzw. Bildweiten hat die Länge e.

Abbildung 3

Der Abstand e ist die Differenz der Bildweite b₁ und b₂:

${\begin{matrix}e&=&b_{1}-b_{2}&&&&&&&{\text{(2)}}\\\end{matrix}}$

Setzt man Gleichung (1) in die Abbildungsgleichung folgendermaßen ein, erhält man:

${\begin{matrix}{\frac {1}{f}}&=&{\frac {1}{g}}+{\frac {1}{b}}\\\ \\{\frac {1}{f}}&=&{\frac {g+b}{g*b}}\\\ \\gb&=&gf+bf\\\ \\(d-b)b&=&(d-b)f+bf\\\ \\b^{2}-db+df&=&0\\\ \\\rightarrow b_{1},_{2}&=&{\frac {d}{2}}\pm {\sqrt[{}]{{\frac {d^{2}}{4}}-df}}\\\ \\\rightarrow d&\geq &4f\\\end{matrix}}$

(Dies ist der Grund, warum Gegenstand und Bild mindestens einen Abstand der vierfachen Brennweite haben sollten.)

Setzt man nun b₁ und b₂ in Gleichung (2) ein, erhält man folgenden Ausdruck:

${\begin{matrix}e&=&2\cdot {\sqrt[{}]{{\frac {d^{2}}{4}}-df}}\\\ \\e^{2}&=&d^{2}-4df\\\ \\\rightarrow f&=&{\frac {d^{2}-e^{2}}{4d}}\\\ \\\end{matrix}}$

Man braucht folglich nur den Abstand d und die Strecke e, um die Brennweite einer Linse zu bestimmen. Diese beiden Werte sind relativ einfach zu bestimmen.

Aufbau

• 1 optische Bank ( ideal 2m)
• 1 Spannungsquelle
• 1 Lichtquelle (z.B. Halogenlampe mit Glühwendel)
• 1 Sammellinse (z.B. 100mm)
• 1 Schirm
• 3 Reiter (Lichtquelle,Linse,Schirm)

Man sollte die Justierung der Höhe von Lichtquelle, Linse und Schirm auf dem Reiter vorab einstellen, da dieses zeitaufwendig ist. Hat man dies vorab unternommen, sollte man die Schüler/innen darauf hinweisen, keine weiteren Höhenverstellungen während der Versuchsdurchführung vorzunehmen.

Durchführung

1. Die Lichtquelle am Besten so fest fixieren, dass das Halogenleuchtmittel bei einer Höhe von genau 10 cm auf der optischen Bank festgeschraubt wird. Bei der Experimentierleuchte im Labor war das Leuchtmittel ca. 1,6 cm tief in der Lampe. In dem Fall musste der Reiter auf einer Höhe von 8,4 cm (rechts vom Reiter) eingestellt werden.

2. Den Schirm auf die Höhe von 90 cm auf der optischen Bank einstellen. Bei den Reitern im Labor wurde der Schirm in der Mitte der Reiter fixiert. Die Reiter selbst waren 5 cm breit, d.h. man musste jeweils 2,5 cm hinzu bzw. weg addieren. (Am Besten sollte auch hier rechts vom Reiter die Höhe eingestellt werden. Möchte man also den Schirm auf eine Höhe vom 80 cm einstellen, muss man demzufolge den Reiter auf 102,5 cm einstellen.)

3. Die Sammellinse (10 cm Brennweite) nun zwischen Leuchte und Schirm stellen und soweit auf der Bank verschieben, bis ein scharfes Bild auf dem Schirm entsteht. Die Höhe rechts vom Reiter notieren (es geht auch hier links vom Reiter, aber eine einheitliche Versuchsdurchführung ist für die Schüler/innen leichter nachvollziehbar und daher wohl sinnvoll.)

4. Die zweite Position der Linse auf der optischen Bank finden und auch hier rechts vom Reiter die Höhe bestimmen. (Hat man bei 3. rechts gemessen, dann muss man auch bei 4. rechts messen, da man den Abstand beider Linseneinstellungen braucht.)

5. Die Schüler den Versuch wiederholt durchführen lassen mit weiteren Höheneinstellungen des Schirms in 10 cm Schritten (bis z.Bsp. 160 cm).

6. Den Versuch mit einer anderen Sammellinse wiederholen (z.Bsp. Brennweite 15 cm).

Ergebnisse

Messung mit der Linse der Brennweite f = 10cm

Messung 1	b1 in cm	b2 in cm	e in cm	d in cm
1	24,60	57,40	32,80	58,20
2	23,95	68,00	44,05	68,20
3	23,65	78,45	54,80	78,20
4	23,35	88,75	65,40	88,20
5	23,15	98,95	75,8	98,20
6	23,05	109,05	86,00	108,20
7	22,95	119,20	96,25	118,20
8	22,8	129,30	106,50	128,20
9	22,75	139,30	116,55	138,20
10	22,70	149,40	126,70	148,20

Messung mit der Linse der Brennweite f = 15cm

Messung 2	b1 in cm	b2 in cm	e in cm	d in cm
1	33,40	58,00	24,60	68,20
2	31,50	69,90	38,40	78,20
3	30,40	81,05	50,65	88,20
4	29,95	91,85	61,90	98,20
5	29,35	101,90	72,55	108,20
6	29,00	112,45	83,45	118,20
7	28,80	122,65	93,85	128,20
8	28,50	132,90	104,4	138,20
9	28,40	143,25	114,85	148,20
10	28,30	153,20	124,90	158,20

Auswertung

Folgende Werte für die Brennweiten wurden bestimmt:

Messung 1: $f=(9,95\pm 0,37)cm$

Messung 2: $f=(14,84\pm 0,35)cm$

Man kann klar erkennen, dass die Methode nach Bessel sehr gute Ergebnisse erzeugt.

Vorteile des Besselverfahrens gegenüber der Nutzung der Abbildungsgleichung:

Nutzt man die Abbildungsgleichung, d.h. man bestimmt g (Gegenstandweite) und b (Bildweite), muss man in Kauf nehmen, dass man mit mehr Unsicherheiten arbeiten muss und somit auch eine eventuell höhere Messunsicherheit beim Ergebnis der Brennweitenbestimmung hat. Die Methode nach Bessel gibt zumeist genauere Ergebnisse in einem kleineren Fehlerintervall und außerdem ergeben sich während der Messung weitaus weniger Messunsicherheiten. Schaut man sich z.Bsp. an, wie man die Gegenstandsweite bestimmen muss, ist das gar nicht so einfach, wie es auf den ersten Blick erscheint, da man nur die Stellung des Reiters messen kann. Die Stellung der Linse kann also nicht direkt gemessen werden. Durch diesen Umstand muss definitiv mehr Messunsicherheit in Kauf genommen werden. Bei kleinen Gegenstandsweiten kann diese Unsicherheit zu großen Abweichungen der Brennweite führen. Abschließend kann man sagen, dass das Besselverfahren eine gute Alternative zur Messung mit der Abbildungsgleichung ist. Das Verfahren ist außerdem gut als Schülerversuch geeignet und somit zu empfehlen.

Sicherheitshinweise

Es sind keine besonderen Sicherheitsmaßnahmen zu treffen.

Siehe auch

Artikel mit ähnlichen Inhalt Geometrische Optik TEST, Optische Bank: Brennweiten Bestimmung