Beschleunigungssensor im Smartphone
| Beschleunigungssensor im Smartphone | |
 Mit seinen integrierten Sensoren kann das Smartphone Beschleunigung und Kreisfrequenz auf dem Plattenspieler messen | |
| Kurzbeschreibung | |
|---|---|
| Mit dem Beschleunigungssensor und dem Gyroskop eines Smartphones lassen sich Radialbeschleunigung und Kreisfrequenz auf einem Plattenspieler mehrdimensional messen. | |
| Kategorien | |
| Digitales Messen, Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Physik der Kreisbewegungen und Radialkräfte. Doppeljahrgangsstufe 9/10 „3.8 Kraft und Beschleunigung“ bzw. 11 LK 4.1 Felder: Bewegung eines Massepunktes. |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Franz Boczianowski |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
Mit dem Beschleunigungssensor und dem Gyroskop eines Smartphones lassen sich Radialbeschleunigung und Kreisfrequenz auf einem Plattenspieler mehrdimensional messen. Mit Hilfe von lässt sich die Position des Beschleunigungssensors vektoriell bestimmen. Für den Unterricht sind unterschiedliche Reduktionen und Differenzierungen möglich.
Inhaltsverzeichnis
Didaktischer Teil
Bedeutung digitaler Medien
Die digitale Datenverarbeitung ist die Kerntechnologie unsere Zeit. Sie betrifft wirtschaftliche, gesellschaftliche und private Lebensbereiche. Es ist für Gegenwart und Zukunft elementar in diesem Bereich Kompetenzen zu besitzen und weiterzuentwickeln. Es ist Aufgabe der Schule, die Schülerinnen und Schüler dementsprechend vorzubereiten. Die Kultusministerkonferenz hat mit ihrem Strategiepapier „Bildung in der digitalen Welt“ (8. Dezember 2016, https://www.kmk.org/aktuelles/thema-2016-bildung-in-der-digitalen-welt.html Stand: 17.06.2017), dafür die Weichen gestellt und sieht diese „digitalen“ Kompetenzen, wie auch das Lesen, Schreiben und Rechnen, als Kulturtechnik an. Abgesehen von fächerübergreifenden Fertigkeiten im Umgang mit elektronischer Datenverarbeitung und digitalen Medien, die es in der Schule zu vermitteln gibt, wie zum Beispiel der Umgang mit Textverarbeitung, Tabellenkalkulation und der zielgerechten und sicheren Nutzung des Internets, werden zukünftig auch fachspezifische Kompetenzen im Umgang mit digitalen Daten zu formulieren sein.
Dieser Beitrag fokussiert auf den Umgang mit Messdaten aus Schulexperimenten und ihrer fachgerechten Aufbereitung, Darstellung und Interpretation. Er adressiert damit die klassischen Kompetenzen des Physikunterrichts (Berliner Rahmenlehrplan, http://bildungsserver.berlin-brandenburg.de/rlp-online/c-faecher/physik/kompetenzen-und-standards/ Stand: 17.06.2017):
- „Erkenntnisgewinnung“ hinsichtlich „Naturwissenschaftliche Untersuchungen durchführen: Auswertung und Reflexion“ und „Elemente der Mathematik anwenden: mathematische Verfahren anwenden“ und
- „Kommunikation“ mit „Informationen erschließen: Informationen aus grafischen Darstellungen entnehmen“
Bedeutung digitaler Werkzeuge beim Experimentieren
Der Umgang mit Messdaten und ihrer Aufbereitung steht in enger Verbindung mit der digitalen Datenverarbeitung. Denn die elektronische Aufnahme und digitale Verarbeitung von Messwerten, zeigt sowohl technische aber auch didaktische Vorteile.
In technischer Hinsicht ist zu nennen, dass eine Vielzahl elektronischer Sensoren für alle Einsatzbereiche existiert. In Kombination mit universelle Aufnahmegeräten können themenübergreifend und einheitlich Daten digital erfasst und aufbereitet werden.
Der Aufbau und die Durchführung von Experimenten ist einfacher zu realisieren, spart Zeit und die Einarbeitung in spezielle und auch kostenintensive Messgeräte.
Die digitale Messungen ermöglichen es, große Datenmengen in hoher zeitlicher Dichte oder Dauer aufzunehmen und machen so große Datenmengen in hoher zeitlicher Dichte oder Dauer aufzunehmen, die bisher außerhalb der Reichweit einer Schulgerätesammlung lagen.
Die Messdaten können einfach gespeichert, vervielfältigt und verteilt werden. Neue System machen sogar eine „data sharing“ zeitgleich zur Messung möglich.
Abgesehen davon, dass die elektronische Datenverarbeitung von Messwerten in allen aktuellen Naturwissenschaften Standard und somit zeitgemäß und authentisch ist und die Verwendung von Smartphones, Tablets und Computern auch Anknüpfungspunkte zur Lebenswelt der Schülerinnen und Schüler herstellt, lassen sich auch didaktische Vorteile ausmachen. Durch die Verwendung digitaler Werkzeuge beim Experimentieren, wie zum Beispiel Messwerterfassungssysteme der Lehrmittelfirmen oder wie in diesem Artikel Smartphones, stehen den Schülerinnen und Schülern in umfangreicher aber zugleich kompakter und handhabbarer Form Messwerten zur Interpretation zur Verfügung. Damit kann der unterrichtliche Schwerpunkt zu „höheren“ Kompetenzen, wie Interpretation experimenteller Daten, verschoben werden.
All dies setzt selbstverständlich das Verständnis des Auswertungsvorgangs voraus. Sicherlich ist es dafür notwendig, das Vorgehen der Messwertaufnahme und Auswertung kleinschrittig, mit „Papier und Bleistift“ und in einer überschaubaren Anzahl von Messwerten zu durchzugehen und zu üben. Um jedoch auch in der Deutung und Interpretation von Messungen Routine zu entwickeln, zum Beispiel im Lesen und Verstehen von Diagrammen, müssen eben auch in diesem Kompetenzbereich viele und reichhaltige Lerngelegenheiten geschaffen werden.
Ein weiterer didaktischer Vorteil liegt in der unmittelbaren zeitgleichen Visualisierung der Messwerte in Diagrammen zur Durchführung des Experiments. Die Beobachtungen wie Bewegungen, Auslenkungen etc. können von den Schülerinnen und Schülern im direkten zeitlichen Zusammenhang gesehen werden: Das Diagramm „wächst“ mit dem Experiment und entwickelt seine charakteristische Gestalt.
Neben dem beschriebenen Feld der Auswertung und Darstellungen von Messwerten eröffnet die elektronische Messwerterfassung durch ihre hohe Datendichte und Qualität außerdem einen Zugang zur statistischen Betrachtung von Messunsicherheit, der weit über die Betrachtung schultypischer „Zick-Zack-Graphen“ hinausgeht.
All diese Aspekten lassen sich auch mit Blick auf die „Kompetenzen in der digitalen Welt“ (ebd.) sehen. So werden mit der digitalen Erfassung und Aufbereitung von Messwerten aus Schulexperimenten die Kompetenzbereiche
- „Suchen, Verarbeiten und Aufbewahren“ hinsichtlich der Kompetenz „Auswerten und Verarbeiten: Informationen und Daten analysieren, interpretieren und kritisch bewerten“ und
- „Problemlösen und Handeln“ bezüglich der Kompetenz „Algorithmen erkennen und formulieren: Eine strukturierte, algorithmische Sequenz zur Lösung eines Problems planen und verwenden“ angesprochen.
Das Smartphone auf dem Plattenspieler als Beispiel für eine digitale Messung
Ein modernes Smartphone (im weiteren SP) besitzt ein Vielzahl an Sensoren. Zur Bestimmung der Ausrichtung des Smartphones, z.B. für die automatische Anpassung des Bildschirms oder für die Steuerung von Spielen, sind ein sogenannter Beschleunigungssensor und meist ein Gyroskop verbaut. Die Sensoren sind miniaturisiert und als Mikrochips auf der Platine nicht identifizierbar. Aber mit einem „physikalischen Trick“ lässt sich die Position des Beschleunigungssensors (im weiteren g-Sensor) im Smartphone bestimmen. Rotiert das Smartphone z.B. auf einem Plattenspieler, lässt sich über die radiale Beschleunigung der Abstand des Sensors zur Rotationsachse bestimmen. Als ergebnisoffene Aufgabe wurde diese Fragestellung von Studierenden im Experimentierpraktikum des ersten Semesters an der Humboldt-Universität im Wintersemester 2016/17 bearbeitet.
Die Übersichtlichkeit der Frage, des Vorgehens und der Berechnungen stehen der Schwierigkeit gegenüber, Kalibration, Unsicherheiten und Störungen zu beherrschen. Dies schafft Lerngelegenheiten gerade im Hinblick auf Generierung von Erkenntnis aus einem Experiment.
Für den Schulunterricht lässt sich das Experiment als Demonstrationsexperiment durchführen. Unterschiedliche Smartphones können vermessen und die Messwerte über das Internet an die Schülerinnen und Schüler verteilt werden. Die Auswertung des Experiments ist auf unterschiedlichen Niveaus möglich und reicht von einer qualitativen Lokalisierung des g-Sensors bis zu einer zweidimensionalen Ortsbestimmung. (Siehe auch Sidney Mau, Francesco Insulla, Elliot E. Pickens, Zihao Ding and Scott C. Dudley (2016) Locating a smartphone's accelerometer. In The Physics Teacher 54, 246. http://dx.doi.org/10.1119/1.4944372)
Schulische Einordnung
Die Physik der Kreisbewegung und der Radialkraft ist Thema der Mittelstufe: In Berlin
„3.8 Kraft und Beschleunigung“ der Doppeljahrgangsstufe 9/10. Im Rahmenlehrplan sind Messungen mit „Beschleunigungs- oder Kraftsensoren“ explizit genannt. Die Radialkraft wird beschrieben durch oder im schulischen Kontext . Was bedeutet, dass sich ein Körper bei konstanter Bahngeschwindigkeit auf einer Kreisbahn bewegt, wenn eine konstante Kraft auf ihn rechtwinklig zu seiner Bahn, also in Richtung des Mittelpunkts, wirkt. Das Smartphone erfährt diese Zentripetalkraft durch die Haftung am Plattenteller.
Versuchsanleitung
Funktionsweise eines Beschleunigungssensors
Die Bezeichnung „Beschleunigungssensor“ und die in SPs häufig verwendete Maßeinheit g ist missverständlich und für den Unterricht problematisch. Befindet sich das SP (in Bezug auf das Klassenzimmer) in Ruhe, sind damit Geschwindigkeit und Beschleunigung gleich Null.
Denn es gilt . Dennoch wird eine Beschleunigung von +1g bzw. vom Gerät angezeigt. Lässt man das SP fallen, zeigt es Kräftefreiheit also Schwerlosigkeit an, doch gerade jetzt bewegt es sich beschleunigt in Richtung Erdboden. Die Ursache ist klar. Die Beschleunigung des SP wird über die Kraft auf den Probekörper im Gerät bestimmt.
Tatsächlich ist der Aufbau eines g-Sensor einfach zu verstehen, weil er mechanisch funktioniert. Eine an Federn aufgehängter Probekörper wird (durch Trägheit oder Gravitation) ausgelenkt und die Auslenkung kapazitiv bestimmt. (Siehe z. B. Video, Bosch, Pressematerial, http://videoportal.bosch-presse.de/clip/_/-/-/Funktionsprinzip-Beschleunigungssensor?category=Connected-Mobility, Aufruf: 17.06.2017). Eine Beschleunigung des SPs nach rechts führt im mitbewegten System zu einer Auslenkung des Probekörpers in entgegengesetzter Richtung, also nach links. (Das mitbewegte Koordinatensystem ist ein Rechtssystem. Die x-Komponente ist nach rechts, die y-Komponente nach oben und die z-Komponente senkrecht zum Display ausgerichtet. Siehe http://phyphox.org/de/unterstutzte-sensoren/ Aufruf: 21.08.2017)
Analog dazu ist die angezeigte Beschleunigung bei einer Kreisbewegung zum Mittelpunkt hin ausgerichtet. Die Gravitationskraft führt auch bei Ruhelage zu einer Auslenkung und das SP zeigt eine konstante „Beschleunigung“ entgegen der Richtung der Schwerkraft. In einigen Physik-Apps wird der Einfluss der Erdanziehungskraft herausgerechnet. Dies ist allerdings nur unter hypothetischen Randbedingungen möglich, da das Gerät seine Ausrichtung im Gravitationsfeld der Erde nicht kennt. Es entstehen unweigerlich Artefakte.
Aufbau
Vorbereitung der digitalen Messung
Die Handhabung von phyphox ist gut dokumentiert und einfach. Auf dem zu vermessenden Smartphone muss die App installiert sein. Sie ist für Android und iOS verfügbar. (http://phyphox.org/de/download-de/ Stand: 17.06.2017)
Über eine WLAN-Verbindung (z. B. per WLAN Tethering des SP) lässt sich phyphox von einem PC aus fernsteuern. Die Messwerte lassen sich auf dem PC in unterschiedlichen Formaten speichern und anschließend (z. B. über eine Cloud) an die Schülerinnen und Schüler verteilen.
Zur Bestimmung der Position des g-Sensors im Smartphone über die o. g. Formel müssen die Kreisfrequenz und die Kraft auf den Probekörper des Sensor bestimmt werden. (Die Masse des Probekörpers kürzt sich nach heraus.) In phyphox lässt sich ein „eigenes Experiment“ anlegen, um die Messwerte von g-Sensor und Gyroskop abzufragen und zu speichern.
Geräte & Materialien
- Smartphone mit Gyroskop und App phyphox (http://www.phyphox.org)
- PC mit WLAN
- Plattenspieler (ideal mit Direktantrieb und Stroboskop) alternativ kugelgelagerter Drehteller
- zur horizontalen Ausrichtung: Papierstreifen 0,2mm, Wasserwaage
Mit einem Plattenspieler als rotierendem System erhält man gute Ergebnisse und einen übersichtlichen Aufbau. Steht kein Plattenspieler zur Verfügung, lässt sich das Experiment auch mit einem gutgelagerten Drehteller durchführen. Einmal in Bewegung versetzt, erhält man zu jeder gemessenen Beschleunigung die zugehörige Kreisfrequenz. Ein Antrieb mit einem Experimentiermotor ist schwierig, da dieser bei niedrigen Drehzahlen häufig unrund läuft. Von hohen Drehzahlen ist wiederum abzusehen, da die Sensoren des SP nur für den Bereich kalibriert sind, in dem sie für gewöhnlich verwendet werden. Das bedeutet, dass je nach Gerät Beschleunigungen jenseits von 1g unter Umständen nicht mehr korrekt angezeigt werden.
Es ist zu beachten, dass nicht alle Smartphones über ein Gyroskop verfügen. In dem Fall ist die Drehzahl extern zu bestimmen. Verwendet man einen Plattenspieler lässt sich die Kreisfrequenz einfach aus der Einstellung (33 und 45 Umdrehungen pro Minute) berechnen. Bestimmt man die Drehzahl extern, verliert das Experiment jedoch an seinem Charakter als digitales Experiment.

Abbildung 1: Mit seinen integrierten Sensoren kann das Smartphone Beschleunigung und Kreisfrequenz auf dem Plattenspieler messen.
Justage und Störungen
Es ist notwendig, den Plattenspieler und das SP exakt horizontal auszurichten. Die „störende“ Gravitationskraft wirkt dann einzig und vollständig entlang der senkrechten Komponente.
Eine Abweichung von der Horizontalen hat unterschiedliche Konsequenzen. Abbildung 2 und Abbildung 3 zeigen die Spezialfälle für einen ausschließlich justierten Plattenspieler bzw. SP. Im ersten Fall ist der y-Anteil der Gravitation im System des SP konstant und führt zu einem konstanten Versatz der Messung (Offset). Im zweiten Fall „wandert“ ein Teil der Gravitationskraft durch die x‘- und y‘-Komponenten des mitbewegten Bezugssystems (Oszillation).
Zur Justage des Plattenspielers auf ein Zehntelgrad genügt eine gute Wasserwaage. Die Justage des SP ist aufwändiger. Nicht nur die Schale des SP ist häufig uneben und die Kamera steht hervor, auch der Plattenteller ist meist nicht völlig plan. Zur Ausrichtung des SP lässt sich ebenfalls phyphox verwenden, indem der g-Sensor (z. B. mit einer geringen Rate von 1 Hz) abgefragt und angezeigt wird. Dicke Papierstreifen (0,2mm) eigenen sich zur Justage.
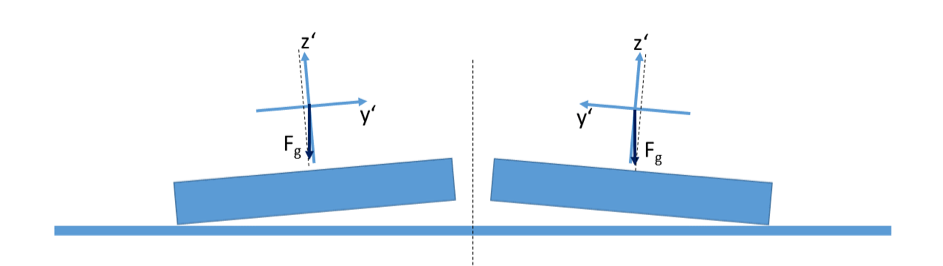
Abbildung 2: Für ein nicht-horizontales SP auf einem horizontalen Plattenspieler ist die y‘-Komponente der Gravitation für jede Ausrichtung konstant.
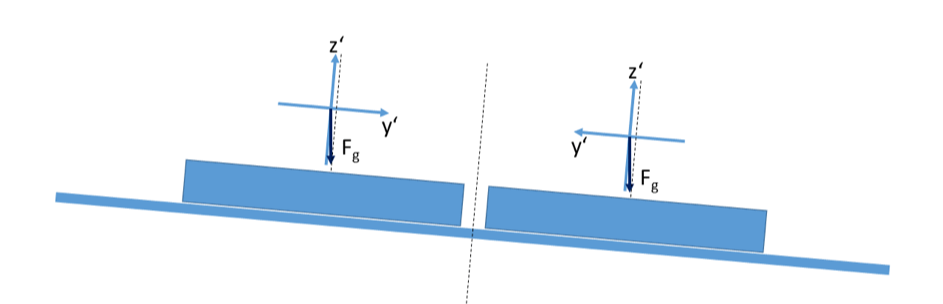
Abbildung 3: Im Fall eines nicht-horizontalen Plattenspieler oszilliert die y‘-Komponente der Gravitation. Hier zu sehen: links positiv und rechts negativ.
Durchführung
Das SP wird an den Stift auf den Plattenspieler gelegt. Es hat sich bewährt, das SP vor jeder Messung für eine Sekunde in Ruhe auf dem Plattenspieler liegen zu lassen. Die Messung wird am PC ausgelöst. Zur Bestimmung des Offsets werden über einige Sekunden Messwerte aufgenommen. Erst dann wird der Plattenspieler gestartet und die eigentliche Messung für einige Umdrehungen aufgezeichnet. Der Plattenspieler wird gestoppt und die Messung am PC beendet. Die Messwerte werden z. B. im Excel-Format gespeichert und ausgewertet, indem abschnittsweise die Mittelwerte für die horizontalen Komponenten der Beschleunigung und die senkrechte Komponente der Kreisfrequenz bestimmt werden. Die Messung werden für unterschiedliche Orientierungen des SP auf dem Plattenteller und unterschiedlichen Drehzahlen aufgenommen.
Ergebnisse
Im Ergebnisteil werden die Messwerte, z.B. in Tabellen (bei quantitativen Versuchen), bzw. die gemachten Beobachtungen (bei qualitativen Versuchen) beschrieben.
Auswertung
Abbildung 4 zeigt eine Beispielmessung mit 33 Umdrehungen pro Minute (rpm). Das SP liegt mit der Oberseite an der Drehachse, der Mittelwert der y‘-Komponente der Beschleunigung ist positiv, also nach innen gerichtet. Trotz der peniblen Justage des SP ist eine Oszillation mit einer maximalen Amplitude von 0,1 um den Mittelwert ay =1,17 deutlich zu erkennen. Abbildung 5 zeigt die Messung für die gleiche Drehzahl, jedoch mit entgegengesetzter Ausrichtung des SPs, also mit der Unterseite an der Achse. Die y‘-Komponente ist folglich jetzt negativ. Der Mittelwert beträgt jetzt ay = -0,79 und fällt damit vom Betrag her geringer aus in der Messung zuvor. Dies erlaubt bereits den ersten Schluss, dass der g-Sensor in der zweiten Messung näher an der Achse liegen muss. Er muss sich in der Unterseite des Telefons befindet. Im Unterricht lasst sich dieses Vorgehen weitertreiben. Mit zwei weiteren Messungen mit der linken und rechten Seite des SP an der Achse, lässt sich auf diese Weise schnell und übersichtlich der Quadrant ausmachen, in dem sich der g-Sensor befindet. Der didaktische Schwerpunkt liegt hierbei für die Schülerinnen und Schüler im Deuten der vier Diagramme.
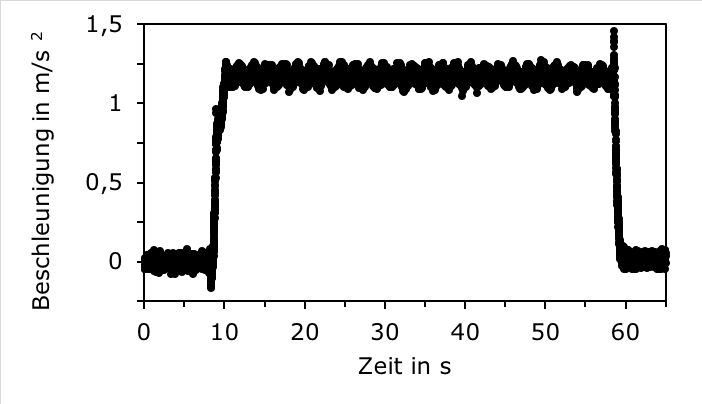
Abbildung 4: Aufgetragen ist die y‘-Komponente der Beschleunigung über der Zeit, gemessen auf einem Plattenspieler mit 33rpm. Das SP liegt mit der Oberseite an der Achse des Plattentellers, die Beschleunigung ist dementsprechend positiv.
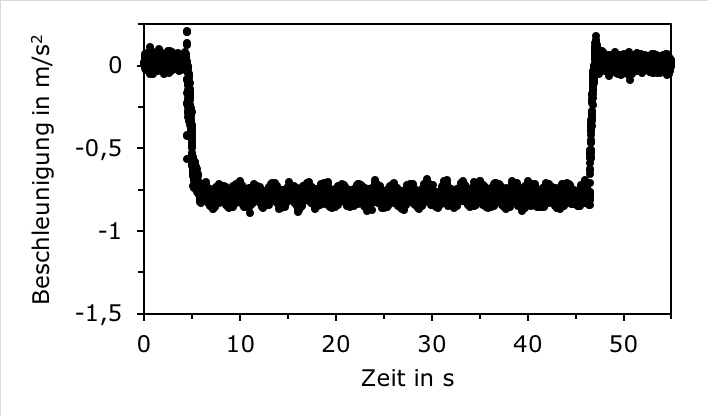
Abbildung 5: Wieder ist die y‘-Komponente der Beschleunigung bei 33 rpm aufgetragen. Diesmal liegt das SP jedoch mit der Unterseite an der Achse. Die Beschleunigung ist negativ und fällt vom Betrag geringer aus.
Trigonometrische Bestimmung
Für die Ortsbestimmung des g-Sensors ist genau genommen nur eine Messung notwendig, da das SP die Beschleunigung in alle Raumrichtungen misst. Zusammen mit dem x-Komponente der Beschleunigung ax = 0,41 lässt trigonometrisch die Position über berechnen.
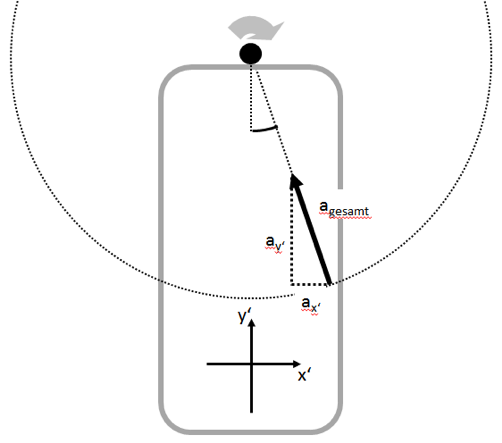
Abbildung 6: Geometrie und Koordinatensystem des SP, das mit seiner Oberseite an der Achse liegt. Aus der Gesamtbeschleunigung lässt sich der Abstand des g-Sensors zur Achse berechnen. Aus den Komponenten die Lage auf dem Kreisbogen.
Diskussion und Bewertung
Da die Position des g-Sensors eines beliebigen Smartphones nicht bekannt ist, ist die direkte Kontrolle des Messergebnisses nicht möglich. Das mag zwar unbefriedigend wirken, weil sich somit nicht aufdecken lässt, „wie gut man gemessen hat“, was für ein Schulexperiment zumeist die unausgesprochene, geheime Forschungsfrage gewesen ist. Ganz im Gegensatz dazu ist das Fehlen eines Referenzwertes für ein naturwissenschaftliches Experiment vielmehr der Normalfall und somit authentisch. Erst die Unüberprüfbarkeit des Ergebnisses macht die Betrachtung von Messunsicherheiten nachvollziehbar. In den Naturwissenschaften ist es üblich ein Vergleichsexperiment, das idealerweise eine andere Methode nutzt, durchzuführen, sodass sich die Experimente gegenseitig stützen. Diese Möglichkeit besteht hier ebenfalls. Die bestimmte Position des Beschleunigungssensors lässt sich prüfen, indem das Smartphone mit dem Beschleunigungssensor direkt auf die Achse des Plattentellers gelegt werden. Hier sollte die Beschleunigung verschwinden.









