Berechnung des Ausdehnungskoeffizienten von Luft
| Berechnung des Ausdehnungskoeffizienten von Luft | |
 Abb. 1: Aufbau des Experimentes | |
| Kurzbeschreibung | |
|---|---|
| Das Experiment zeigt die Ausdehnung von Luft bei Temeraturerhöhung. Anschließend kann der räumliche Ausdehnungskoeffizient berechnet werden. | |
| Kategorien | |
| Thermodynamik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 9-10, Sek. II |
| Basiskonzept: | Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment, Schüler*innen-Experiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Sylvia Kowalski |
| Kontakt: | sylvia.kowalski@cms.hu-berlin.de |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Tobias Ludwig |
Das Experiment gehört zum Teilgebiet der Wärmelehre und befasst sich mit der Ausdehnung eines Gases bei Erwärmung. Es wird Luft in einem Glaskolben erwärmt, welches mit einem U-Manometer verbunden ist. Die Flüssigkeit in diesem U-Manometer wird durch die Volumenzunahme der Luft im Glaskolben verschoben. Zusätzlich kann somit qualitativ der Ausdehnungskoeffizient von Luft nachgewiesen werden.
Inhaltsverzeichnis
Didaktischer Teil
In diesem Teil werde ich mich mit dem Umgang von Messunsicherheiten im Schulunterricht beschäftigen. Dabei werde ich auf ein Sachstrukturmodell eingehen, welches Julia Hellwig in ihrer Dissertation "Messunsicherheiten verstehen" (siehe Hellwig [1] (2012), Kapitel 9) beschreibt.
1. Existenz von Messunsicherheiten
Grundsätzlich ist es wichtig, den Schülerinnen und Schülern klarzumachen, dass jede Messung eine Unsicherheit mit sich bringt und dass die Ergebnisse nie fehlerfrei gemessen werden können (vgl. Hellwig[1] S. 171). Es ist also wichtig, schon vor dem Experiment mögliche Fehlerquellen mit den Schülerinnen und Schülern zu besprechen. In diesem Experiment wären die Bestimmung des Volumens des Rundkolbens und des Glasrohres, sowie die Messung der Temperatur und das Ablesen des Wasserstandes am Maßstab, Beispiele für messbare Unsicherheiten. Das Experiment wird aber auch von Umweltfaktoren wie der Temperatur, dem Luftdruck, Schwingungen und sonstigen zufälligen Ereignissen beeinflusst (vgl. Hellwig [1] S.171). Diese sind schwer zu berechnen, aber es ist dennoch wichtig sie mit den Lernenden zu diskutieren um ihnen ein Verständnis für mögliche Abweichungen vom Literaturwert zu geben. Zudem sollten auch die Begriffe Messunsicherheit und Messabweichung geklärt werden. Eine Messunsicherheit gibt die Genauigkeit eines Ergebnisses an, eine Messabweichung gibt jedoch die Abweichung vom Vergleichswert an (vgl. Hellwig [1] S.173).
2. Einfluss von Messunsicherheiten
Als Nächstes sollte das Ziel des Experimentes diskutiert werden. In unserem Fall ist dass die Berechnung des räumlichen Ausdehnungskoeffizienten von Luft. Im Idealfall wäre das Ziel einen Wert möglichst Nahe am Referenzwert zu bestimmen. Da dies aber durch den Einfluss von Messunsicherheiten selten der Fall ist, konzentrieren wir uns mehr darauf eine geringe Messunsicherheit und somit ein genaueres Messergebnis zu erzielen (vgl. Hellwig [1] S.174). Ein Ergebnis ist nur von Bedeutung wenn sowohl das Messergebnis, als auch die Messunsicherheit bestimmt werden. Die Angabe des Ergebnisses ist in der Form
zu machen (vgl. Hellwig [1] S.176).
3. Erfassung von Messunsicherheiten
Nachdem das Experiment durchgeführt worden ist, werden alle Messunsicherheiten notiert und im Protokoll erklärt. Wichtig ist es, den Schülerinnen und Schülern bewusst zu machen, dass das Erfassen der Messunsicherheiten ein bedeutender Bestandteil des Protokolls ist, da ein Leser somit einen besseren Überblick über den Messprozess und die Verlässlichkeit des Messergebnisses erhält (vgl. Hellwig [1] S.176). Danach geht es an die Berechnung des räumlichen Ausdehnungskoeffizienten von Luft. Da eine Messreihe aufgenommen wurde, ist es sinnvoll den Mittelwert der Messungen zu bilden. Dementsprechend muss auch die Standardabweichung berechnet werden.
Zur Berechnung der Unsicherheiten muss den Schülerinnen und Schülern ein mathematisches Instrument vorgegeben werden, mit dessen Hilfe sie diese ausrechnen können. In diesem Fall ist es die Formel für die Größtfehlerabschätzung.
4. Aussagekraft von Messunsicherheiten
Messunsicherheiten geben die Anzahl der Stellen an, auf die das Messergebnis gerundet werden soll. Das bedeutet, dass sie angeben bis auf welche Stelle man sich bei dem Ergebniswert "sicher" sein kann (vgl. Hellwig [1] S.183). Zum Abschluss kann das Messergebnis nun mit dem Literaturwert verglichen werden. Dabei ist ebenfalls zu beachten, dass es einen Unterschied zwischen der Messunsicherheit und der Messabweichung gibt. Um einen Vergleich zwischen dem Ergebniswert und dem Literaturwert zu machen, wird die Differenz beider gebildet und geschaut ob diese im Bereich der Messunsicherheit liegt (vgl. Hellwig [1] S.184).
Versuchsanleitung
Aufbau
Geräteliste
Folgende Materialien werden zum Aufbau des Experimentes benötigt:
- Rundkolben, 25 ml
- durchbohrter Stopfen
- Stopfen
- 3-Wege-Hahn
- 3 Verbindungsschläuche
- Glasrohr, 5 cm
- 2 Glasröhrchen, 30 cm
- gefärbtes Wasser, 15 ml
- Glasbecher, 1000ml
- Wasserkocher
- digitales Thermometer
- Rührer
- Vertikalmaßstab
- 3 Stativfüße
- 2 Stativstangen, ca. 80 cm
- 1 Stativstange, ca. 60 cm
- 1 Stativstange, ca. 25 cm
- 2 Stativstangen, ca. 15 cm
- 9 verschiedene Klemmen (siehe Abb.2)
- höhenverstellbare Platte
Der Aufbau orientiert sich an der Abb. 1. Auf die höhenverstellbare Platte wird der Glasbecher gestellt. Das mittlere Rohr am 3-Wege-Hahn wird mit einem kurzen Schlauch verbunden. Dieser Schlauch wird an das kurze Glasrohr (5 cm) befestigt, welches mit dem durchbohrten Stopfen zusammengeschlossen wird. Dieser Stopfen wird anschließend mit dem Rundkolben verbunden und verschließt diesen. Eine weitere Öffnung des 3-Wege-Hahns wird mit einem Verbindungsschlauch verbunden und der Schlauch dann an das Glasröhrchen (30 cm) gesteckt. Das andere Ende des Glasrohres wird ebenfalls mit einem Verbindungsschlauch zusammengeschlossen und dieses wiederum mit dem nächsten Glasröhrchen (30 cm). Die Glasröhrchen werden mit Klemmen an den Stativstangen fixiert. In das U-Rohr-Manometer wird das gefärbte Wasser gegossen. Der Rundkolben wird anschließend vollständig in das Wasserbecken getaucht, in dem Wasser von Raumtemperatur ist. Um den Druck konstant zu halten, wird zu Anfang des Experimentes ein Stopfen an die letzte Öffnung des 3-Wege-Hahnes gesteckt.
Durchführung
Als Erstes wird das Volumen des Rundkolbens gemessen. Dazu wird der durchbohrte Stopfen eingesteckt und am unteren Ende eine Markierung gesetzt. Nach der Entfernung des Stopfens wird Wasser (20°C) bis zur Markierung gefüllt und anschließend die Höhe des Wassers an einem Messzylinder abgelesen. Das Innenvolumen des Glasrohres muss ebenfalls ermittelt werden. Dazu wird Wasser (20°C) in das Glasrohr gegossen und anschließend in einen Messzylinder. Um die Volumenzunahme am Maßstab ablesen zu können, berechnen wir das Volumen pro Zentimeter im Glasrohr.
In den Glasbecher wird ein wenig des heißen Wassers zugefügt. Nachdem das Wasser umgerührt worden ist wird die Temperatur abgelesen. Gleich danach wird am Maßstab abgelesen um wie viel das gefärbte Wasser im inneren Glasrohr des U-Rohr-Manometers gesunken ist. Um ein besseres Ergebnis zu erzielen und eine Mittelwertbildung machen zu können, wird dieser Vorgang zehn Mal wiederholt.
Ergebnisse
Die Messung besteht aus zwei Elementen. Zunächst wird die Temperaturerhöhung am Thermometer gemessen und danach der Wasserstand im Glasrohr. Um die Volumenzunahme der Luft berechnen zu können, wird das Volumen pro Zentimeter im Glasrohr (30 cm) berechnet. Dazu wird die Länge des Glasrohres und dessen Volumen benötigt.
Länge des Glasrohres:
Volumen des Glasrohres:
Unter Verwendung der Formel ergibt sich die Umrechnung
Somit kann die Volumenzunahme im Glasrohr unter Verwendung des Dreisatzes berechnet werden.
Der räumliche Ausdehnungskoeffizient kann nun unter der Verwendung der Formel berechnet werden. Dabei ist zu beachten, dass die Temperturdifferenz der End- und der Anfangstemperatur ist. Das Volumen im Rundkolben liegt bei
Insgesamt wurden zwei Messreihen aufgenommen. Die Ergebnisse dieser Messungen wurden in den nachfolgenden Tabellen zusammengefasst.
| T in °C | L in cm | V in ml | in | in |
|---|---|---|---|---|
| 19,9 | 0 | 0 | 0 | 0 |
| 22,3 | 1,1 | 0,29 | 0,0038 | 0,0003 |
| 23,8 | 1,7 | 0,45 | 0,0036 | 0,0003 |
| 25,6 | 2,6 | 0,68 | 0,0037 | 0,0003 |
| 27,4 | 3,3 | 0,87 | 0,0036 | 0,0003 |
| 30,6 | 4,5 | 1,18 | 0,0034 | 0,0002 |
| 33,0 | 6,1 | 1,60 | 0,0038 | 0,0002 |
| 33,8 | 6,5 | 1,71 | 0,0038 | 0,0002 |
| 35,2 | 7,4 | 1,95 | 0,0040 | 0,0002 |
| 36,5 | 8,2 | 2,16 | 0,0041 | 0,0002 |
| T in °C | L in cm | V in ml | in | in |
|---|---|---|---|---|
| 19,5 | 0 | 0 | 0 | 0 |
| 22,0 | 1,2 | 0,32 | 0,0040 | 0,0003 |
| 24,2 | 2,3 | 0,61 | 0,0041 | 0,0003 |
| 27,3 | 3,6 | 0,95 | 0,0038 | 0,0002 |
| 28,9 | 4,2 | 1,10 | 0,0037 | 0,0002 |
| 30,9 | 5,1 | 1,34 | 0,0037 | 0,0002 |
| 31,9 | 5,7 | 1,50 | 0,0038 | 0,0002 |
| 32,9 | 6,2 | 1,63 | 0,0038 | 0,0002 |
| 33,9 | 6,8 | 1,79 | 0,0039 | 0,0002 |
| 35,5 | 7,8 | 2,05 | 0,0040 | 0,0002 |
Anschließend wurde der Mittelwert des Ausdehnungskoeffizienten aus beiden Messreihen berechnet. Es ergeben sich folgende Ergebnisse:
Messreihe 1:
Messreihe 2:
Die Berechnung der Unsicherheiten wird im Kapitel zur Auswertung erläutert.
Auswertung
Die Volumenzunahme von Luft bei Erwärmung verhält sich nährungsweise wie ein ideales Gas, also kann davon ausgegangen werden, dass der räumliche Ausdehnungskoeffizient lautet. Dabei gilt für die maximale Temperatur . Damit kommen wir auf den Wert
- (vgl. Wilke[2] S. 270).
Beim Experiment gibt es eine große Anzahl an Unsicherheiten, eine davon ist an die Berechnung des Volumens im Rundkolben geknüpft. Beim Messen des Volumens entsteht eine Unsicherheit von Ebenfalls gibt es eine Unsicherheit für die Temperaturablesung. Das Ablesen der Temperatur am Thermometer hat eine Unsicherheit von Dies liegt daran, dass die Temperaturanzeige sehr geschwankt ist und die Temperatur im Messbecher an unterschiedlichen Stellen auch verschiedene Werte hatte. Da in der Formel zur Berechnung des Ausdehnungskoeffizienten die Temperaturdifferenz benutzt wird, kommen wir auf eine Unsicherheit von Ebenfalls fehlerbehaftet ist die Volumenmessung des inneren Glasrohres vom U-Manometer. Bei der Ablesung am Maßstab kommt noch ein Fehler von hinzu. Die Unsicherheit des Volumens im Glasrohr ist Die Unsicherheit des Volumens pro Zentimeter ergibt sich aus der Formel Das Ablesen des Wasserstandes am Maßstab ergibt laut Formel den Wert Somit ergibt sich eine gesamte Unsicherheit für die Volumenänderung von .
Die Unsicherheiten für die Ergebnisse der einzelnen Ausdehnungskoeffizienten wurden mit Hilfe der Gaußschen Fehlerfortpflanzung berechnet. Hierzu wurde folgende Formel verwendet:
Altnernativ kann in der Schule die Größtfehlerabschätzung benutzt werden. Die Formel dazu lautet .
Die Berechnung des Mittelwertes erzeugt eine zusätzliche Unsicherheit. Die Standardabweichung liegt bei der ersten Messreihe bei und bei der zweiten Messreihe . Um eine exakte Unsicherheit zu bekommen wurde die Unsicherheiten der einzelnen Ausdehnungskoeffizienten gemittelt. dabei ergab sich bei beiden Messreihen der Wert . Zum Abschluss werden beide Unsicherheiten addiert und ergeben die Unsicherheiten und
Eine weitere Möglichkeit für die Berechnung der räumlichen Ausdehnung ist die graphische Darstellung der Temperatur- und Volumenänderung.
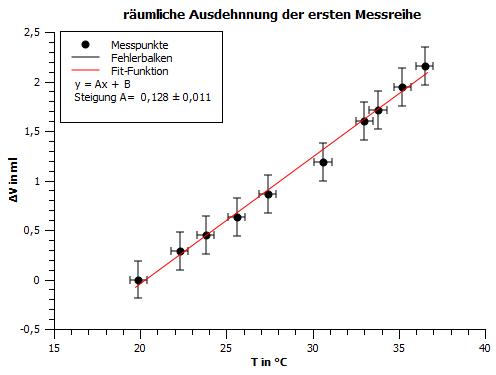
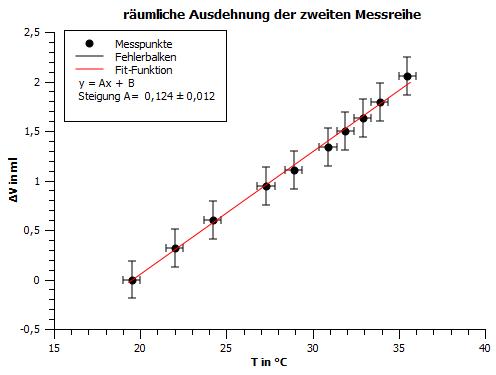
Die Messpunkte der Messreihen wurden linear regressiert. Anhand der Steigung , welche sich aus ergibt, kann der Ausdehnungskoeffizient unter Verwendung der Formel berechnet werden.
Hieraus ergeben sich die folgenden Ergebnisse für den Ausdehnungskoeffizienten
Messreihe 1:
Messreihe 2:
Die Unsicherheiten wurden ebenfalls mit der Gaußschen Fehlerfortpflanzung berechnet. Hierfür wurde folgende Formel benutzt:
Alternativ kann in der Schule wieder über die Größtfehlerabschätzung gerechnet werden. Die dazugehörige Formel lautet .
Die Unsicherheit des Volumens im Rundkolben ist diesselbe wie in der obigen Rechnung und die Unsicherheit der Steigung A kann aus den Abbildungen 3-4 entnommen werden.
Abschließend folgt der Vergleich mit dem Literaturwert.
| experimenteller Wert | graphisch bestimmter Wert | Literaturwert |
|---|---|---|
| in | in | in |
| 0,0038 0,0004 | 0,0040 0,0005 | 0,0037 |
| 0,0039 0,0003 | 0,0039 0,0005 |
Der Literaturwert liegt innerhalb des Vertrauensbereichs der Messung. Dabei ist zu beachten, dass die Berechnung nur eine Näherung ist, da das Volumen V für 0°C definiert ist (vgl. Wilke[2] S. 270). Dieser Versuch eignet sich meiner Meinung nach sehr gut zur Durchführung in der Schule. Die hohen Messunsicherheiten liefern eine gute Grundlage für eine Diskussion zum Thema Messunsicherheiten mit den Schülerinnen und Schülern. Optional kann man in der Schule, zum Thema der idealen Gase, anhand des Experimentes zeigen das sich die Temperatur und das Volumen eines idealen Gases bei konstantem Druck proportional zueinander verhalten. Hierzu müsste das Gesamtvolumen nach jeder Erwärmung berechnet werden und dann das Verhältnis bestimmt werden (vgl. Wilke[2] S. 270).
Sicherheitshinweise
Beim Benutzen des Wasserkochers ist darauf zu achten sich nicht zu verbrennen.
Ebenfalls sollte vorsichtig mit den Glasobjekten hantiert werden. Als Vorsichtsmaßnahme sollten beim Auf- und Abbau Handschuhe getragen werden, falls etwas zu Bruch geht.
Literatur
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 Hellwig, J. (2012): Messunsicherheiten verstehen - Entwicklung eines normativen Sachstrukturmodells am Beispiel des Unterrichtsfaches Physik ; RU Bochum, verfügbar unter RU Bochum [15.04.2016]
- ↑ 2,0 2,1 2,2 Wilke, H. (1997): Physikalische Schulexperimente-Band 1 Mechanik/Thermodynamik; Volk und Wissen Verlag, Berlin