Barometrische Höhenformel im Teilchenmodell
| Barometrische Höhenformel im Teilchenmodell | |
| Kurzbeschreibung | |
|---|---|
| Es wird ein Modellgas mit Stahlkugeln im „Gerät zur kinetischen Gastheorie“ simuliert und auf die Höhenabhängigkeit der Teilchenhäufigkeit untersucht. | |
| Kategorien | |
| Thermodynamik, Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | System, Wechselwirkung, Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | relativ leicher Aufbau aus einfachen Komponenten |
| Informationen | |
| Name: | Alexander Simon |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Ulrike Gromadecki-Thiele |
Die Dichteverteilung eines idealen Gases wird mit der Barometrischen Höhenformel [1] beschrieben. Sie kann dazu verwendet werden um den exponentiellen Abfall von Dichte und Druck mit zunehmender Höhe in unserer Atmosphäre zu erklären. Dieser Sachverhalt soll mithilfe eines makroskopischen Modells nachvollzogen werden. Hierzu werden einige hundert Stahlkugeln in einem speziellen Apparat in Bewegung versetzt und ihre statistische Aufenthaltshäufigkeit in Abhängigkeit von der Höhe über dem Boden mit einer Lichtschranke ermittelt.
Inhaltsverzeichnis
Theoretischer Hintergrund
Grundannahme der Barometrischen Höhenformel ist, dass sich der Druck in einem Gas aufgrund des Eigengewichts der höher liegenden Gasmassen erhöht.
Für ein ideales Gas lässt sich der Druck über die Dichte ausdrücken.
Dabei ist
- die universelle Gaskonstante
- die absolute Temperatur und
- die molare Masse des Gases.
Daraus ergibt sich die Differentialgleichung
mit der allgemeinen Lösung
- .
Durch Logarithmieren dieser Gleichung erhält man die Geradengleichung
- ,
für deren Überprüfung sich ein linearer Fit eignet.
Didaktischer Hintergrund
Ein wesentliches Ziel dieses Experiments ist es, den Schülern die Vorstellung des Teilchenmodells bei Gasen zu erleichtern. Es wird ein theoretisches Modell für ein Ensemble aus einzelnen Molekülen zu Anschauungszwecken makroskopisch nachgebildet. An diesem Aufbau werden Beobachtungen vorgenommen, die mit der Theorie idealer Gase verglichen und dem realen Verhalten der Erdatmosphäre assoziiert werden sollen. Dabei ist es von besonderer Bedeutung, die Modellebenen von der Realität zu trennen um Verwechlungen und Fehlvorstellungen vorzubeugen.
Verschiedene Unteruchungen haben gezeigt, dass gerade die Teilchenstruktur der Materie für viele Schüler ein großes Verständnisproblem darstellt.[2] So herrschen bis zum Ende der Sekundarstufe I Fehlvorstellungen vor, die schon früh und hauptsächlich durch die Übertragung makroskopischer Eigenschaften auf die submikroskopische Welt entstehen. Im Folgenden werden einige für die Modellwelt dieses Experiments relevante Beispiele erläutert.
Das Modell ist ein mit Luft und einigen hundert Stahlkugeln gefüllter quaderförmiger Raum. Es soll damit ein Gaßmoleküle enthaltendes Gefäß modelliert werden. Die Bodenplatte ist beweglich und wird im Betrieb mit einem Elektromotor in Schwingung versetzt. Damit soll eine zeitlich konstante mittlere Geschwindigkeit der Stahlkugeln erreicht werden, wie sie auch in einem statistischen idealen Gas für die Moleküle konstant ist. Diese Form der Energiezufuhr ist notwendig, da anders als in einem idealen Gas die Energieerhaltung der Mechanik aufgrund von Reibung verletzt ist. Hauptursache sind die inelastischen makroskopischen Stöße der Stahlkugeln, aber auch die Luftreibung spielt aus didaktischer Sicht eine wichtige Rolle. Der Grund dafür ist die verbreitete Fehlvorstellung, dass zwischen den Luftteilchen sich immer noch ein Reibung erzeugendes kontinuierliches Medium und somit kein Vakuum befinde.[2] Es sollte also unbedingt mit den Schülern geklärt werden, dass die im Makrokosmos bekannte Luftreibung im Mikrokosmos als Stöße der Luftmoleküle umgedeutet werden muss und dass deshalb zwischen den Luftmolekülen Vakuum herrscht. Die aus dem Makrokosmos bekannte und für Schüler oftmals unumstößliche Regel, dass sich Reibungsverluste nie vermeiden lassen, darf also nicht auf die Ebene einzelner Atome übertragen werden.
Sollte mit dem Modell die Erdatmosphäre oder eine Luftsäule in ihr assoziiert werden, so ist zu beachten, dass Stöße der Kugeln mit den Gefäßwänden und vor allem mit der Gefäßdecke kein Äquivalent zum realen Phänomen besitzen, da die Erdatmosphäre außer dem Erdboden keine harten Begrenzungen hat. Die barometrische Höhenformel wird nach den Gesetzen eines idealen Gases hergeleitet. Sie beruhen auf Annahmen, die reale Gase nicht erfüllen. So wird beispielsweise das Volumen der Gasteilchen vernachlässigt. Aus diesem Grund kann auch darauf hingewiesen werden, dass die barometrische Höhenformel selbst nur ein theoretisches Modell ist, welches die atmosphärische Dichteverteilung nur bis zu einem gewissen Grad beschreiben kann. Eine perfekte Übereinstimmung von Demonstrationsexperiment und Theorie sollte demnach von vornherein nicht angestrebt oder sogar erwartet werden.
Versuchsanleitung
Aufbau
Kugeln und Zubehör
Dieses Experiment arbeitet mit 200 bis 600 kleinen Kugeln aus Glas, Stahl oder Plasik mit einem Durchmesser von ca. 2 mm (1). Aus Gründen der Sauberkeit sollte eine Wanne (2) o.ä. verwendet werden, damit möglichst wenig Kugeln unwiederfinbar verschwinden können. Weitehin sollten für sicheren Transfer Trichter sowie verschließbare Behälter (3) bereitstehen.
Mechanischer Aufbau
Der Hauptgegenstand ist das „Gerät zur kinetischen Gastheorie“ (4) von PHYWE (Artikel-Nr.: 09060-00). Dieses wird zunächst mit den Kugeln befüllt. Dazu wird am Besten ein Trichter verwendet. Bei Glas- und Plastikkugeln kommt es aufgrund ihres geringen Eigengewichts häufiger zu einem Stau bei der Befüllung. In diesem Fall wird mit einem dünnen Stab in die Füllöffnung (5) gestochen und gleichzeitig am Gerät gerüttelt, bis alle Kugeln im Gefäß sind. Da die Einfuhr ins Gefäß sehr knapp über dem Boden liegt, muss bei größeren Kugelmengen das Gerät in eine Schräglage gebracht werden. Es reicht aus, wenn der Gefäßboden mit einer Lage Kugeln bedeckt ist. Es können auch mehr Kugeln verwendet werden. Allerdings entfernt sich dadurch das Modell weiter von der Bedingung des idealen Gases, welche das Teilchenvolumen im Vergleich zum Raumvolumen vernachlässigt. Aus demselben Grund sollte die verschiebbare Gefäßdecke auf maximale Höhe hochgefahren und dort festgeschraubt werden.
Elektrischer Aufbau
Das Gerät zur kinetischen Gastheorie wird an eine Gleichspannungsquelle angeschlossen und mit 9 bis 12 V betrieben. Die Schwingungen des Motors können im Betrieb das Gerät über den Boden wandern lassen. Es sollte also ein möglichst stabiles Stativ und eine gut haftende Unterlage wie z.B eine Gummimatte verwendet werden. Damit muss der Experimentator das Gerät nicht permanent festhalten. Für eine möglichst konstante mittlere Geschwindigkeit der Kugeln wird vom Hersteller eine direkte Messung der Bodenplattenfrequenz mithilfe einer Stroboskoplampe empfohlen [3]. Dafür müssen die Frequenzen von Motor und Lampe aneinander angepasst werden. Die Motorenfrequenz wird durch Nachregelung der Betriebsspannung konstant gehalten, da sie bei einigen Spannungsquellen aufgrund der Erwärmung des Motors im längeren Bertieb stetig abfällt. Alternativ kann die Betriebsspannung auch direkt mit einem Voltmeter überprüft und somit auf das Stroboskoplicht verzichtet werden. In diesem Fall ist eine eventuelle Frequenzmessung nicht mehr möglich. Da das Stroboskoplicht jedoch vom eigentlichen Gegenstand des Versuchs ablenken könnte und die Durchführungszeit weiter streckt, wird an dieser Stelle die Verwendung des Voltmeters empfohlen.
Messtechnischer Aufbau
Die Messung erfolgt mit einer höhenverstellbaren Gabellichtschranke (6). Es ist möglich, die Höhe nach jeder Messung manuell am Stativ zu verstellen. Dies hat sich jedoch als umständlich und ungenau erwiesen. Es wird daher empfohlen, die Lichtschranke auf einer leicht verstellbaren Hebebühne (7) aufzubauen. Die Zählmessung erfolgt entweder direkt in der Lichtschranke, sofern sie über diese Funktion verfügt oder über einen externen Digitalzähler. Die Lichtschranke durchläuft im optimalen Fall die Mitte des Gefäßes, damit die Messung möglichst weit von den nicht vollkommen elastisch stoßenden Wänden erfolgt. Es sollte darauf geachtet werden, dass die Lichtschranke tatsächlich jede Unterbrechung zählt, da beispielsweise eine Zählung alle zwei Durchläufe für Fadenpendel eine gängige Lichtschrankeneinstellung ist. Die Häufigkeitsermittlung erfolgt über einen je nach Anspruch variierbaren Zeitraum, der mit einer Stoppuhr (8) erfasst werden kann.
Durchführung
Für die Messreihe sollten je nach geplantem Zeitumfang sinnvolle Höhen- und Zeitintervalle gewählt werden. Für die Schule ist es ausreichend, alle 2 cm Höhe (7 Einstellungen) für je 30 s zu messen. Der Messzeitraum würde somit ca. 5 Minuten betragen. Sollten weniger als 50 Zählungen auf den höchsten Positionen auftreten, kann dort alternativ auch für einen längeren Zeitraum gemessen werden.
Das Gerät zur kinetischen Gastheorie verfügt über eine eingebaute Millimeterskala. Für die Höhenmessung der Lichtschranke können die oberen Kanten der vorderen und hinteren Gabelarme angepeilt und ihre Höhe an der Skala abgelesen werden. Die Lichtschranke selbst befindet sich etwa einen halben Zentimeter tiefer. Da sich jedoch die absolute Höhe aufgrund der schwingenden Bodenplatte schwer ermitteln lässt und für den zu zeigenden exponentiellen Zusammenhang nicht relevant ist, können auch die systematisch verschobenen Werte verwendet werden. Die Bedeutung des Offsets müsste in diesem Fall jedoch mit den Schülern besprochen werden.
Vor Beginn der Messung sollte der Motor für mindestens 5 s bereits eingeschaltet sein, damit sich die gewünschte Geschwindigkeitsverteilung der Kugeln einstellen kann. Die Messknöpfe der Lichtschranke und der Stoppuhr werden gleichzeitig betätigt. Nach dem zuvor festgelegten Zeitintervall wird die Messung an der Lichtschranke beendet und notiert. Anschließend wird die Stoppuhr zurückgesetzt und die Lichtschranke auf die nächste Messhöhe gefahren. Dieser Vorgang wird solange wiederholt, bis die gewünschte Menge an Messdaten ermittelt ist.
Ergebnisse
Jeder Höhe wird eine Zählung von N Unterbrechungen der Lichtschranke für einen gewählten Zeitraum zugeordnet. Der Zeitraum selbst kann dazu genutzt werden, die Zählungen in eine Zählrate wie z.B. "Zählungen pro Minute" umzurechnen. Das ist insbesondere dann notwendig, wenn unterchiedliche Zeitintervalle für verschiedene Höhen gewählt wurden. Es wird also eine Tabelle mit den Spalten "Höhe", "N", "N/min" angelegt. Werden Unsicherheitsbetrachtungen angestrebt, müsste vor allem hinter "N" und "N/min" etwas Platz dafür gelassen werden. Für die Auswertung sollte noch genug Platz für eine letzte Spalte "ln(N/min)" vorhanden sein.
Auswertung
Die Zählungen bzw. Zählraten werden mit dem erwarteten exponentiellen Verhalten verglichen. Dazu eignet es sich, die Werte zu logarithmieren und zu prüfen, ob grafisch eine Gerade entsteht. Die Unsicherheit jeder Zählung wird nach statistischer Konvention mit abgeschätzt. Dieser Wert wird gegebenenfalls durch die Länge des Messintervalls geteilt um die Unsicherheit für die Zählrate zu erhalten.
Zu guter Letzt gibt der Reziprokwert dieser Unsicherheit an, wie stark der natürliche Logarithmus streut.
Für die Unsicherheit der Höhenwerte gelten die bekannten Konventionen für Längenmessung. Sie ist für dieses Experiment nicht vernachlässigbar.
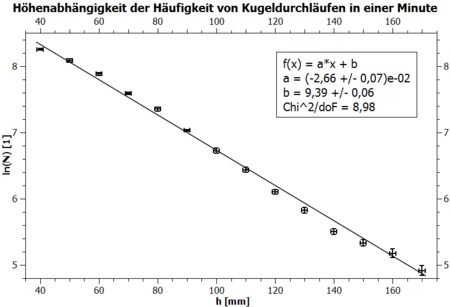
Das Ergebnis lässt sich grafisch darstellen. Hierbei reicht es, den linearen Zusammenhang des Logarithmus zu bestätigen. Damit kann gezeigt werden, dass sich auch makroskopische Kugeln unter vergleichbaren Bedingungen qualitativ so verhalten, wie es von Luftmolekülen erwartet wird. Für die nicht logaritmierte Zählrate bedeutet dies, dass sie mit zunehmender Höhe exponentiell abnimmt. Dieses Ergebnis sollte auch mit kurzen Messzeiten reproduzierbar sein. Eine quantitative Auswertung der Fitparameter wie z.B. dem Geradenanstieg führt dagegen zu weit. Ebenso handelt es sich bei diesem Versuch, wie bereits im didaktischen Hintergrund erwähnt, um einen makroskopischen Nachbau der die Theorie lediglich grob qualitativ bestätigen soll. Eine Diskussion der Vertrauensintervalle ist hierbei also nicht vordergründig.
Sicherheitshinweise
Während des Betriebs heizt sich der Motor stark auf und sollte nicht berührt werden, bevor einige Minuten zum Abkühlen vergangen sind.
Sollten viele Kugeln den Aufbau unbeabsichtigterweise verlassen und auf dem Fußboden landen, besteht Ausrutschgefahr. Sie sollten sobald wie möglich aufgefegt werden.
Literatur
- ↑ Vogel, H. (1999): Gerthsen Physik; 20. Auflage, Springer Verlag, Berlin, S. 224
- ↑ 2,0 2,1 Mikelskis-Seifert, S. et al (2003):Die Bedeutung des Denkens in Modellen
bei der Entwicklung von Teilchenvorstellungen –
Stand der Forschung und Entwurf einer Unterrichtskonzeption;Zeitschrift für Didaktik der Naturwissenschaften; Jg. 9, 2003, S. 75-88 Referenzfehler: Ungültiges
<ref>-Tag. Der Name „Mikelskis-Seifert“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ Versuchsanleitung zur Barometrischen Höhenformel mit dem „Gerät zur kinetischen Gastheorie“ von PHYWE (Artikel-Nr.: 09060-00): http://repository.phywe.de/files/versuchsanleitungen/p2140700/e/p2140700.pdf [19.09.2016]