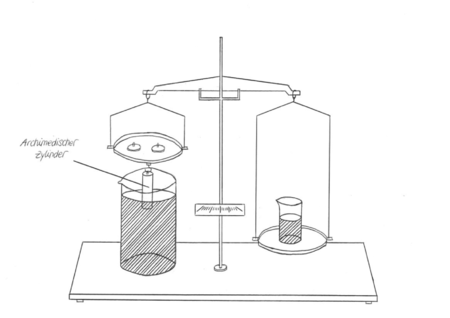
Archimedischer Zylinder
| Archimedischer Zylinder | |
 Archimedischer Zylinder | |
| Kurzbeschreibung | |
|---|---|
| Bauteil für präzise Messungen zur Bestimmung von Auftriebskräften in verschiedenen Flüssigkeiten | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 7 |
| Basiskonzept: | System, Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Tom Leonhardt |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Johannes Schulz |
Das archimedische Prinzip ist eines der ältesten, grundlegendsten und bedeutsamsten Prinzipien der mechanischen Physik und wurde bereits vor über 2000 Jahren, von dem nach ihm benannten Mathematiker und Physiker Archimedes (* 287 v. Chr., † 212 v. Chr.), entdeckt und bewiesen. Mit Hilfe des Archimedischen Zylinders lässt sich dieses Gesetz leicht nachzuvollziehen und vor allem sehr gut veranschaulichen. Ziel ist es, mit dem Archimedischen Zylinder indirekt zu zeigen, dass die Auftriebskraft eines Körpers in einer Flüssigkeit genauso groß, wie die Gewichtskraft der von ihm verdrängten Flüssigkeit ist, indem man die Masse des verdrängten Wassers mit der Masse, die benötigt wird, um den Auftrieb des Körpers zu kompensieren, misst und anschließend vergleicht. Der Archimedische Zylinder besteht aus einem Kunststoffzylinder, der genau in einen Metallbecher hineinpasst.
Inhaltsverzeichnis
Didaktischer Teil
Für die meisten Schüler stellt der Begriff „schwimmen“ nichts Neues dar. Doch sind die Schülervorstellungen dazu in der Regel falsch. Häufige Antworten, die man in diesem Zusammenhang bekommt, sind: „Weil der Gegenstand von der Luft angezogen wird.", "Nein, der Baumstamm ist zu schwer und schwimmt nicht." (vgl. Hardy, Möller, Jonen, Stern, (2002), S. 63) [1]. Diese Antwort ist jedoch nicht die physikalische Erklärung dafür, warum ein Körper schwimmt oder nicht. Darüber hinaus sind die falschen Alltagsvorstellungen, falls vorhanden, der Schülerinnen und Schüler häufig so stark gefestigt, dass man diese nur schwer wieder revidieren kann. (vgl. Hardy, Möller, Jonen, Stern, (2002), S. 64) [2] An diesem Punkt sollte man das archimedische Prinzip im Unterricht einführen. Denn über das von Archimedes entdeckte Phänomen, kann man die Bedingungen, die ein Körper benötigt um zu schwimmen, definieren. Folgende Begriffe spielen hierbei eine große Rolle: Dichte, verdrängtes Medium, Gewichtskraft des verdrängten Mediums, Kraft bzw. Kräfteverhältnis. All diese Begrifflichkeiten sollten den Schülerinnen und Schülern bekannt und vorher im Unterricht behandelt worden sein, da man aus diesen Begriffen die Auftriebskraft herleiten kann. Denn die Auftriebskraft ist der Grund dafür, warum Körper im Wasser schwimmen können.
Die Auftriebskraft, die ein Körper in einem Medium erfährt, ist genauso groß, wie die Gewichtskraft des von ihm verdrängten Mediums. Ist die Auftriebskraft des Körpers größer als seine Gewichtskraft, dann schwimmt ein Körper. Ist sie kleiner als die Gewichtskraft, dann sinkt der Körper. Sind beide Kräfte gleich groß, begibt sich der Körper in einen Schwebezustand. Da man die Auftriebskraft eines Körpers nur sehr schwer direkt messen kann, nutzt man das Archimedische Prinzip und berechnet die Auftriebskraft über die Gewichtskraft des vom Körper verdrängten Wassers. Denn laut dem archimedischen Prinzip sind die beiden Kräfte gleich groß. Außerdem ist die Auftriebskraft in einem Schwerefeld der Gewichtskraft genau entgegengerichtet. (vgl. Dahocke, Götz, Langensiepen, (2000), S. 92) [3]
Für die Lernenden stellt sich besonders am Anfang immer das große Problem dar, die verschiedenen Größen richtig zu unterscheiden und anzuwenden. Besondere Schwierigkeiten entstehen in der Regel beim Erschließen der Gewichtskraft der verdrängten Flüssigkeit und diese anschließend mit der Auftriebskraft gleichzusetzen. Diese Analogie ist für viele Lernende nicht intuitiv und stellt sie deswegen vor Probleme. Außerdem sind die anderen Verfahren (Verdrängungsmethode, Abmessen und Errechnen, Umlenkrolle mit Federkraftmesser, etc.) zur Dichte- bzw. Auftriebsbestimmung nicht anschaulich genug und können das Phänomen des archimedischen Prinzips nicht direkt veranschaulichen.
Anders ist es mit dem archimedischen Zylinder, da er genau dieses Phänomen erkennbar macht und man beide Kräfte, getrennt voneinander, in einem Experiment veranschaulichen kann. Das Experiment kann den Lernenden dabei helfen den Transfer von der Gewichtskraft der verdrängten Flüssigkeit hin zur Auftriebskraft des Körpers zu schaffen. Darüber hinaus wird im Experiment deutlich, dass beide Größen bzw. die gemessen Werte theoretisch gleich groß sind. In der Praxis treten natürlich, je nach Versuchsaufbau und Durchführung, Abweichungen auf. Man benötigt keine langen Messreihen (siehe Aufbau und Durchführung), sondern kann in wenigen Schritten und mit geringem Zeitaufwand die relevanten Messgrößen aufnehmen. Den einzigen Nachteil den dieses Experiment mit sich bringt, ist die Tatsache, dass man einen sehr präzisen Aufbau und eine ruhige Arbeitsweise benötigt, da man sonst keine brauchbaren bzw. präzisen Ergebnisse erwarten kann.
Der simple Aufbau und die leicht zu verstehende Funktionsweise machen dieses Experiment in jeder Klassenstufe anwendbar, wenn das Vorwissen der Schülerinnen und Schüler auf gegebenen Niveau ist. Es eignet sich vor allem dann gut, um die Thematik des archimedischen Prinzips einzuführen und verständlich zu machen. Der Vorteil des archimedischen Zylinders, im Gegensatz zu den anderen Verfahren, ist der einfache Aufbau. Dadurch, dass der Zylinder exakt in den Metallbecher hineinpasst, besitzen beide das gleiche Volumen. Somit sollten bei den Schülerinnen und Schülern keine Fehlvorstellungen entstehen. Die Schülerinnen und Schüler sollten in der Lage sein zu erkennen, dass der Kunststoffzylinder genauso viel Flüssigkeit verdrängt, dem das Füllvolumen des Metallbechers entspricht. Wiederum hieraus sollte es für die Schülerinnen und Schüler hilfreich sein zu erkennen, dass die Auftriebskraft genauso groß wie die Gewichtskraft des verdrängtem Mediums ist, da somit die Dichte, das Volumen und die Erdbeschleunigung in beiden Fällen die selben Werte annehmen. An dieser Stelle des Unterrichts könnte man eine Verbindung zwischen der Dichte eines Körpers und der Auftriebskraft herstellen, falls nicht schon geschehen. Denn "Die Auftriebskraft ist gleich dem Produkt aus der Dichte ρ der Flüssigkeit, dem Ortsfaktor g und dem Volumen V des ein- oder untergetauchten Teils des Körpers:." (Dahocke, Götz, Langensiepen, (2000), S. 92) [4] Somit ist die Auftriebskraft auf der Erde von zwei Größen abhängig. Dabei hat die Dichte und das Volumen Einfluss darauf, wie ein Körper sich in seinem Medium verhält. Da das Produkt aus Dichte und Volumen, der physikalischen Größe Masse entspricht, können zwei Fälle betrachtet werden. Zum einem bleibt das Volumen konstant, zum anderen bleibt die Dichte konstant. In Fall 1 entscheidet, die Dichte darüber, ob ein Körper schwimmt oder nicht. Im zweiten Fall gibt, bei konstanter Dichte, das Volumen des Körpers bzw. des verdrängten Mediums Aufschluss darüber, wie der Körper sich in seinem Medium verhält. Über diese Ansätze kann man die Abhängigkeiten der Auftriebskraft von seinen einzelnen Faktoren erklären.
Wie man dabei vorgeht steht in der Verantwortung der Lehrkraft. Am besten lässt sich das Experiment als Demonstrationsexperiment im Unterricht implementieren, obwohl es genauso gut als Schülerexperiment genutzt werden könnte, jedoch stellt sich in diesem Fall die große Menge an Material als große Hürde dar.
Aufbau
Folgende Materialen werden für den Aufbau des Experiments benötigt:
- - Hydrostatische bzw. Tarierwaage mit 2 Waagschalen
- - Archimedischer Zylinder - bestehend aus Metallbecher und Kunststoffzylinder
- - Wägesatz 10mg ... 200g
- - Becherglas 600ml
- - Becherglas 100ml
- - verschiedene Flüssigkeiten
Für den Aufbau des Experimentes orientiere man sich an der Abbildung 1. Zuerst wird die hydrostatische Waage mit den zwei Waagschalen aufgebaut. Anschließend werden zwei verschiedene Messungen durchgeführt. Zuerst sollte man die Auftriebskraft, die der Zylinder in einer Flüssigkeit erfährt, messen. Hierzu wird der Kunststoffzylinder an eine der beiden Waagschalen gehangen. Auf die andere Waagschale wird ein Becherglas mit einem Füllvolumen von 100ml abgestellt. Anschließend tariert man die Waage durch Eingießen einer Flüssigkeit, welche untersucht wird, in das 100ml Becherglas aus. Falls es möglich ist einen Feinabgleich durch Tarierschrauben an der Waage durchzuführen, sollte man dies tun.
In der zweiten Messungen wird die Gewichtskraft der verdrängten Flüssigkeit gemessen. Für diesen Teil des Experimentes wird nur der leere Metallbecher des archimedischen Zylinders gegen den Kunststoffzylinder ausgetauscht. Wieder muss die Waage austariert werden, indem man das 100ml Becherglas mit Wasser füllt. Auch hier ist ein Feinabgleich durch die Trierschrauben, falls möglich, durchzuführen.
Durchführung
Bei der Durchführung dieses Experimentes werden zwei Messungen durchgeführt. Bei der ersten Messung wird die Auftriebskraft des Zylinders bzw. die Masse zur Kompensation der Auftriebskraft des Zylinders gemessen. In der zweiten Messung wird die Gewichtskraft bzw. die Masse des Wassers, welches sich im Metallbecher befindet, gemessen. Am Ende jeder Messungen erhält man zwei Messwerte von Massen, die miteinander verglichen werden können, und Aufschluss über den Zusammenhang von Auftriebskraft eines Körpers und der Gewichtskraft des vom Körper verdrängten Mediums gibt.
1.) Für die Bestimmung der Auftriebskraft, die auf den Zylinder wirkt, muss die Waage austariert sein (siehe Aufbau). Nun wird der Archimedische Zylinder in das, mit einer Flüssigkeit, gefüllte Becherglas (600ml) vollständig eingetaucht, da sonst eine Oberflächenspannung entsteht, welche Messergebnisse verfälscht. Nun wird die hydrostatische Waage aus dem Gleichgewicht geraten. Das am Anfang hergestellte Gleichgewicht an der Waage wird nun durch Auflegen von Massestücken auf die Waagschale, an welcher der Zylinder befestigt ist, wieder hergestellt. In diesem Fall ist die Auftriebskraft des Zylinders genauso groß, wie die Gewichtskraft der aufgelegten Massestücke. Nun werden die benötigten Wägemassen bzw. die gesamt aufgelegten Massen () notiert und später zur Berechnungen der Auftriebskraft verwendet. Diese Messung kann nun für beliebig viele Flüssigkeiten in der selben Art und Weise wiederholt werden.
Um die Auftriebskraft des Archimedischen Zylinders in der Flüssigkeit zu bestimmen, wird folgende Gleichung verwendet:
2.) Im zweiten Teil des Experimentes tauscht man den Kunststoffzylinder gegen den leeren Metallbecher, welcher ebenfalls unten an der Waagschale befestigt wird, aus. Auch in diesem Fall muss die Waage wieder austariert sein (siehe Aufbau), damit man die Messung starten kann. Nach dem Austarieren der Waage muss der Metallbecher mit der Flüssigkeit, die man untersuchen möchte, bis an den obersten Rand gefüllt werden, so dass die Wasseroberfläche mit der Becheroberkante flach abschließt. Mit dem Befüllen des Metallbechers wird die hydrostatische Waage in ein Ungleichgewicht fallen. Nun wird durch erneutes Auflegen von Massestücken, auf die Waagschale mit dem 100ml- Becherglas, die Waage austariert und man notiert sich die Masse () der aufgelegten Massenstücken. Diese aufgelegten Massestücken entsprechen der Masse der Flüssigkeit im Metallbecher. Wenn man nun die beiden Kräfte berechnet, kann man die Gewichtskraft der Flüssigkeit mit der Auftriebskraft des Zylinders vergleichen. Genau wie bei der ersten Messung kann diese Messung für verschiedene Flüssigkeiten wiederholt werden.
Die Gleichung für die Berechnung der Gewichtskraft der verdrängten Flüssigkeit lautet:
Messunsicherheiten
Da das Experiment nur qualitativ durchgeführt wurde, werden die Messunsicherheiten auch nur qualitativ betrachtet. Aufgrund der sehr präzisen Arbeitsweise, die dieses Experiment verlangt, treten mehrere Messunsicherheiten auf, die das Ergebnis verfälschen können. Deswegen ist es von großer Bedeutung, dass man die hydrostatische Waage möglichst präzise aufbaut und anschließend das Austarieren sehr genau vornimmt, um somit große Abweichungen zu vermeiden. Andererseits könnten hier bereits erste große Fehler auftreten, die sich dann auf die weiteren Messungen übertragen bzw. fortpflanzen. Obwohl man an dieser Stelle betonen sollte, dass es oft sehr subjektive Einschätzungen sind, was "präzise" und "genau" bedeutet.
Genau wie beim Aufbauen und Vorbereiten können bei den eigentlichen Messungen ebenfalls Messfehler auftreten. Zuerst wäre da die bereits genannte Messunsicherheit durch die Oberflächenspannung, die auftreten würde, wenn man den Zylinder bei der ersten Messung der Auftriebskraft nicht komplett in die Flüssigkeit absenkt. Eine weitere Messunsicherheit, die man mit großer Sicherheit immer mit in die Fehlerberechnung einbeziehen sollte, ist die Tatsache, dass jede Masse auch von einer Messunsicherheit betroffen ist. Des Weiteren besitzen die Massenstücke nur bestimmte Massen, was ein sehr genaues Arbeiten einfach nicht möglich macht. Diese Faktoren sollten jedoch nur zu einem kleinen Messfehler führen. Ebenfalls von nicht geringer Bedeutung ist die subjektive Wahrnehmung, wann sich ein System im Gleichgewicht befindet und wann nicht. Dieser Fehler wird jedoch umso kleiner, je präzisier man mit der hydrostatischen Waage arbeiten kann bzw. die Waage es zulässt.
Bei der zweiten Messung stellt vor allem das Befüllen des Metallbechers, verbunden mit dem anschließenden Anbringen an die Waage, ein Problem dar. Es ist sehr schwierig, den Metallbecher zum einen bis zum oberen Rand aufzufüllen (auch hier spielt die subjektive Wahrnehmung eine Rolle) und zum anderen so anzubringen, dass man keinen Flüssigkeitsverlust hat. Diese beiden Faktoren sind jedoch schwierig zu quantifizieren. Letztendlich sind bei dieser Messung die selben Messunsicherheiten, wie Unsicherheit der Massen, das Problem mit dem : „Wann stellt sich das Gleichgewicht ein?“ und die Präzision der hydrostatischen Waage, vorhanden.
Ergebnisse
Auch bei den Ergebnissen muss betont werden, dass die Versuchsreihen nur qualitativ betrachten werden, da keine konkrete quantitative Erfassung der Messwerte mit anschließender Fehlerbetrachtung und -rechnung vorgenommen wurde. Es erfolgte lediglich eine qualitative Durchführung des Experiments, da keine hydrostatische Waage vorhanden war und deshalb eine selbst gebaute Waage genutzt werden musste. Diese Waage lies jedoch keine präzisen Messungen zu, weshalb auf eine quantitative Messung verzichtet wurde.
Man kann jedoch sagen, dass die erzielten Ergebnisse im Rahmen der gegebenen Möglichkeiten, während der Durchführung des Experimentes, positiv ausfielen, da bei jeder Messung das gewünschte Ergebnis eingetreten ist. Es entstand in beiden Messungen ein erkennbares Gleichgewicht zwischen den Waagschalen. Außerdem konnte festgestellt werden, dass sich die aufgelegten Massen, welche benötigt wurden, um die Auftriebskraft des Zylinders zu kompensieren, in etwa mit den Massen übereinstimmte, die man im zweiten Teil des Experiments auf die Waagschale auflegen musste, um die Masse der im Metallbecher befindlichen Flüssigkeit zu bestimmen.
Um sich einen Überblick von einer quantitativen Messung zu machen, wird auf das Leybold-Heft Physik Mechanik , Versuch Nr. 1.8.2-1 verwiesen. Dort kann man eine Tabelle mit Messwerten finden, die unter Einbindung von Messunsicherheiten berechnet wurden. Jedoch sollte man diese Messwerte stets hinterfragen und kritisch betrachten , da dort keine Angaben gemacht wurden, unter welchen Bedingungen die Messungen durchgeführt wurden.
Auswertung
Man kann festhalten, dass sich der Archimedische Zylinder als solides Experimentierwerkzeug herausgestellt hat, da man mit seiner Hilfe das Archimedische Prinzip im Schulunterricht ohne großen Zeitaufwand (falls alle Materialen vorhanden sind), leicht und verständlich erläutern kann.
Es gibt zwei ähnliche Messungen, die sich jedoch in der Tatsache unterscheiden, dass sie zwei verschiedene Kräfte untersuchen wollen, die jedoch in einem engen Zusammenhang stehen. Um die Auftriebskraft des Kunststoffzylinders zu bestimmen, wird der Körper an eine Waagschalen angehangen und komplett in eine Flüssigkeit abgesenkt, wodurch die hydrostatisch Waage aus dem vorher hergestellten Gleichgewicht gerät. Um dieses Ungleichgewicht wieder in ein Gleichgewicht zu verwandeln, muss man die Auftriebskraft durch die Gewichtskraft von zusätzlich aufgelegten Massen kompensieren. Dies funktionierte gut erkennbar und man konnte den Vorgang "des sich an das Gleichgewicht annähern" deutlich erkennen und nachvollziehen.
Bei der zweiten Messung wird die Gewichtskraft der verdrängten Flüssigkeit des Körpers bestimmt. Hierzu wird der Kunststoffzylinder gegen einen Metallbecher ausgetauscht, in welchen der Zylinder genau hinpasst. Der Metallbecher kann demnach genau das Volumen des Zylinders fassen. In den Metallbecher wird die zu untersuchende Flüssigkeit eingefüllt. Genau wie bei der ersten Messung, gerät die Waage in ein Ungleichgewicht. Dieses Ungleichgewicht entspricht jedoch nicht dem erwünschten Ergebnis, denn nur wenn sich die Waage in einem Gleichgewicht befindet, ist die Gewichtskraft, die an der Waagschale mit dem Metallbecher zieht, genauso groß, wie die Gewichtskraft, die auf die andere Waagschale wirkt. Auch bei dieser Messung ist der Vorgang zur Herstellung des Gleichgewichts der hydrostatischen Waage deutlich erkennbar.
Wenn man abschließend die gemessenen Massen bzw. die errechneten Kräfte mit einander vergleicht, wird man erkennen können, dass die zur Kompensation der Auftriebskraft erforderliche Masse () genauso groß ist, wie die Masse () der verdrängten Flüssigkeit. Aus den weiteren Berechnungen wird darüber hinaus deutlich, dass die Auftriebskraft eines Körpers genau der Gewichtskraft des vom ihm verdrängten Wassers entspricht. Hiermit ist das Archimedische Prinzip erläutert und man kann Aussagen über das Verhalten eines Körpers in einem bestimmten Medium treffen. Darüber hinaus kann man Ableitungen und Verbindungen zwischen diesem Verhalten des Körpers und seiner Stoffeigenschaft "Dichte" und dem Volumen des Körpers ziehen.
Sicherheitshinweise
Beim Aufbau und der Durchführung des Experiments sind keine besonderen Hinweise zur Sicherheit zu geben. Lediglich zu erwähnen wäre an dieser Stelle der Umgang mit den Flüssigkeiten, die man untersucht. Es könnten unter Umständen Flüssigkeiten untersucht werden, die gesundheitsschädlich sind. Aus diesem Grund muss die Lehrkraft die Schülerinnen und Schüler auf die Gefahr hinweisen und genaue Instruktionen für den Umgang mit den Flüssigkeiten geben!
Literatur
- ↑ Hardy, J.; Möller, K.; Jonen, A.; Stern, E. Warum schwimmt ein Baumstamm?. in: Physik Journal 1. (2002), 3. Ausgabe. Universität Münster
- ↑ Hardy, J.; Möller, K.; Jonen, A.; Stern, E. Warum schwimmt ein Baumstamm?. in: Physik Journal 1. (2002), 3. Ausgabe. Universität Münster
- ↑ Dahocke, H.; Götz, R.; Langensiepen, F. (2000). Handbuch des Physikunterrichts Sekundarbereich I - Band 2, Mechanik II: Hydro - und Aerostatik, Akustik, Kinematik, Dynamik, Flugphysik. Aulas Verlag Daubner & CO KG: Köln
- ↑ Dahocke, H.; Götz, R.; Langensiepen, F. (2000). Handbuch des Physikunterrichts Sekundarbereich I - Band 2, Mechanik II: Hydro - und Aerostatik, Akustik, Kinematik, Dynamik, Flugphysik. Aulas Verlag Daubner & CO KG: Köln