Addition von Kräften
| Addition von Kräften | |

| |
| Kurzbeschreibung | |
|---|---|
| Dieses Experiment gehört in die Mechanik. Es kann zur Veranschaulichung der (vektoriellen) Addition von Kräften im Unterricht genutzt werden. | |
| Kategorien | |
| Newtonsche Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. I und II |
| Basiskonzept: | Wechselwirkungen |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment, Schülerexperiment |
| Anzahl Experimente in dieser Unterkategorie | 2 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | René Kunzendorf |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Dr. Franz Boczianowski |
Die Vorstellungen der Schülerinnen und Schüler (kurz: SuS) vom Begriff Kraft werden sehr stark von ihren Erfahrungen im Alltag geprägt. Normalerweise erleben wir die Kraft als eine Form von Zug oder Schub auf einen Körper. So könnte man sagen, dass wir beim ziehen eines Schlittens oder schieben eines Autos eine Kraft auf einen anderen Körper ausüben. Dieses Experiment soll eine Situation betrachten, bei der mehr als eine Kraft auf einen einzelnen Körper wirken. Die SuS sollen dabei den Begriff Nettokraft kennen lernen und verstehen, dass sich mehrere Kräfte gegenseitig kompensieren können (Nettokraft gleich null).
Inhaltsverzeichnis
Einordnung in den Rahmenlehrplan
In der Doppeljahrgangsstufe 9/10 wird innerhalb des Pflichtbereichs P4 - Schneller werden und Bremsen, der Kraftbegriff eingeführt (Zitat:vgl. Senatsverwaltung für Bildung, Jugend und Sport, Berlin, 2006: Seite 45). Dazu gehört neben den Newton´schen Axiomen auch die experimentelle Anwendung dieser. In der Sekundarstufe II wird die Mechanik im Bereich "Bewegung eines Massepunktes" in Grund- und Leistungskurs noch einmal aufgegriffen. Da hier der Fokus allerdings auf der Bewegung im Gravitionsfeld liegt, könnte das Experiment mehr am Rande durchgeführt werden, um das mathematische Arbeiten mit Vektoren in der Physik zu vertiefen. [5]
Da die Experimente in der Sekundarstufe I und II durchgeführt werden können, werde ich im Folgenden auf beide Jahrgangsstufen eingehen.
Fachlicher Schwerpunkt
Kräfte erleben wir in vielen verschiedenen Formen und anhand einer Vielzahl von Beispielen. Für die SuS wird der Begriff "Karft" häufig zunächst eindimensional und im Zusammenhang mit der gleichmäßig beschleunigten Bewegung eingeführt, sodass die SuS die Beschleunigung eines Körpers auf das wirken einer Kraft zurückführen können.
Kernpunkt dieses Experiments ist das Superpositiosprinzip für Kräfte. Dabei wird das Experiment sowohl für die Sekundarstufe I und II mit unterschiedlichen herangehensweisen und Lernzielen betrachtet werden. In der Sekundarstufe II wird der fächerübergreifende Anwendungsbezug auf die zugrunde liegende Mathematik im Vordergrund stehen. Dazu wird der fachliche Hintergrund kurz geklärt.
Mathematische Anwendung des Superpositionsprinzips
Das zweite Axiom beschreibt den Fall, dass auf einen Körper eine oder mehrere Kräfte wirken, welche sich zu einer auf den Körper wirkenden Nettokraft vektoriell addieren lassen.
In diesem Fall kann man beobachten, dass diese Nettokraft eine Beschleunigung zur Folge hat und ihre Richtung vorgibt. Dabei ist der Betrag der Beschleunigung abhängig von der Masse des Körpers und der auf ihn einwirkenden Nettokraft. Dieser Zusammenhang kann wie folgt formuliert werden:
Die Beschleunigung eines Körpers ist direkt proportional zu der auf ihn wirkenden Nettokraft und umgekehrt proportional zu seiner Masse.
Die Richtung der Beschleunigung ist identisch mit der Richtung der wirkenden Nettokraft. [1]
- ,
- ,
wobei Σ F die Summe aller wirkenden Kräfte ist.
Die SI-Einheit der Kraft ist Newton (1 N) und lässt sich gut aus dieser Gleichung ableiten. So ergibt sich aus der Beschleunigung (m/s²) und der Masse (kg) die Einheit für die Kraft. Es gilt:
Dies können die SuS auch selbst erschließen, da sie bereits die Einheiten der Beschleunigung und der Masse kennen.
Da eine Kraft eine gerichtete Größe ist, muss sie als Vektor interpretiert werden. Im kartesischen Koordinatensystem kann man damit die Beschleunigung in die Richtungen x, y und z wie folgt berechnen:
Gelegentlich werden in der Schulphysik Situationen betrachtet, in denen mehr als eine Karft auf einen Körper wirkt. Das Ziel ist es, die Nettokraft, welche sich durch die Vektorsumme aller angreifenden Kräfte berechnen lässt, zu bestimmen. Dafür können alle Kraftvektoren, die auf den Körper wirken eingezeichnet werden, wobei der betroffene Körper als Massepunkt dargestellt wird. Dabei entspricht die Länge des Vektors dem Betrag der Kraft.
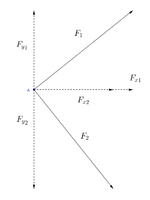
Die Nettokraft lässt sich sowohl geometrisch als auch rechnerisch ermitteln. In Skizze 1 sind die Kräfte F1 und F2 in ihre x und y-Komponenten zerlegt worden. Diese lassen sich dann leicht addieren und ergeben die Komponenten der Nettokraft. Durch ausmessen der Länge des Vektors kann der Betag der Kraft bestimmt werden.
Rechnerisch lässt sich über Winkelbeziehungen sowohl der Betrag der resultierenden Nettokraft berechnen, als auch die Richtung der Kraft bestimmen.
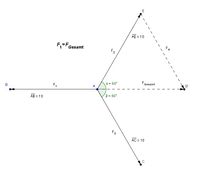
In Skizze 2 sind 3 Kraftvektroen eingezeichnet. Verschiebt man nun F3 in den Punkt E kann man direkt die Richtung des aus F2 und F3 entstehenden Kraftvektors FGesamt ablesen kann.
Die Länge von FGesamt lässt sich zum Beispiel über den Kosinussatz berechnen. Auf dieses Bespiel bezogen ergibt das:
Daraus folgt:
Anwendung der Newton´schen Axiome - Reibung
Ein weiteres Anwendungsgebiet der Newton´schen Axiome ist die Reibung. Die Reibung kann unterschieden werden in Haft,- Gleit- und Rollreibung und berechnet sich aus dem Reibungskoeffizienten μ und der Normalkraft. Dabei ist der Reibungskoeffizient abhängig von der Art der Reibung und welche Stoffe dabei beteiligt sind. Allgemein kann man sagen, dass der Rollreibungskoeffizient in der Regel so klein ist, dass die dadurch entstandene Reibung vernachlässigt werden kann.
Da in dem Experiment die Beschleunigung ermittelt werden soll, ist vor allem die Gleitreibung von Interesse. Diese ist immer der Bewegungsrichtung des Körpers entgegengesetzt und berechnet sich wie folgt:
Dabei wird für die Reibung von Papier auf Stahl für den Reibungskoeffizient μG = 0,3 gewählt.
Didaktischer Teil
Notwendiges Vorwissen der Schüler
Für die Sekundarstufe 1 sollten für die Addition von Kräften das erste und zweite newton´sche Axiom in der eindimensionalen Form bekannt sein. Sollte die Graviationskraft nicht bekannt sein können die Kräfte auch über einen Federkraftmesseer bestimmt werden. Für die geometrische Bestimmung der Nettokraft müssen die zweidimensionale Darstellung von Kräften sowie ihre Zerlegung bekannt sein.
Für die Sekundarstufe 2 werden des Weiteren die Begriffe der Normalkraft und der Gleitreibung benötigt, sofern man das Experiment auch qualitativ untersuchen möchte.
Sollen die SuS Berechnungen zu den Winkeln und der wirkenden Nettokraft durchführen müssen zusätzlich aus der Mathematik der Vektorbegriff, die trigonometrischen Sätze (im besonderen der Kosinussatz) bekannt sein.
Schülervorstellungen
Wie bereits erwähnt sind die Vorstellungen von vielen physikalischen Vorgängen sehr stark von unseren Alltagserfahrungen geprägt. Bezogen auf das Experiment gibt es zwei Situationen, die genauer betrachtet werden müssen.
Kraft und Aktivität
Eine sehr häufig auftretende Fehlvorstellung ist, dass die SuS einem ruhenden Körper keine Kraft zuordnen. Das heißt, dass die SuS in aktive (i.d.R. sich bewegende) und passive (ruhende) Körper. Dabei kann nur ein aktiver Körper auch eine Kraft ausüben. Dieses Problem lässt sich sehr gut im ersten Teil des Experiments thematisieren (siehe Aufbau und Durchführung), da auf den ruhenden Puck augenscheinlich 3 Kräfte wirken müssen. [3][4]
Kraft und Bewegung
In diesem Fall wird von vielen SuS einem Körper, der sich bewegt, eine Kraft zugeordnet. Dabei kommt es häufig zu der Proportionalität zwischen Bewegung und Kraft, d.h. ein Körper mit einer höheren Geschwindigkeit besitzt auch eine höhere Kraft. Auch wird die Kraft häufig mit der Endgeschwindigkeit verknüpft - je höher die Endgeschwindigkeit, desto größer muss die wirkende Kraft gewesen sein. Dabei wird die Beschleunigung über eine längere Strecke überhaupt nicht betrachtet.
Da die Beschleunigung des Pucks im zweiten Teil des Experiments nur über eine sehr kurze Strecke erfolgt kann es an dieser Stelle ebenfalls zu dieser Fehlvorstellung kommen. [3][4]
Differenzierung und didaktische Reduktion
Sekundarstufe I
Das Experiment lässt sich in der Sek I gut nach der Einführung der Newtonschen Axiome durchführen. Die SuS haben i.d.R. Newton I - III eindimensional kennengelernt, sodass mit diesem Experiment der 2-dimensionale Fall mit mehreren Kräften besprochen werden kann.
Da in der 9. bzw. 10 Klasse sowohl die Trigonometrie und der Vektorbegriff noch nicht zwingend in der Mathematik behandelt worden sind muss man an dieser Stelle auf umfassende Berechnungen verzichten. Dafür lässt sich der Versuch geometrisch betrachten.
Ziel des Versuchs sollte es sein den SuS zu veranschaulichen wie mehrere Kräfte auf einen Körper wirken und welchen Einfluss die Richtung der Kraft auf die resultierende Nettokraft hat.
Merksätze für die Schüler:
- (Eine Kraft kann durch einen Pfeil veranschaulicht werden, wobei die Länge des Pfeils dem Betrag der Kraft entspricht und der Angriffspunkt gleich dem Ursprung des Pfeils ist.)
- Wirken mehrere Kräfte auf einen Körper, so addieren sich diese zu einer wirkenden Nettokraft. Diese lässt sich durch zerlegen der einzelnen Kräfte betsimmen.
- Verharrt ein Körper in seiner Ruheposition, obwohl mehrere Kräfte auf ihn wirken, so ist die Nettokraft gleich "null".
- Wird ein Körper durch zwei oder mehr Kräfte beschleunigt, so bewegt er sich in die gleiche Richtung wie die, in welche die Nettokraft wirkt.
Sekundarstufe II
In der Sekundarstufe II sind die mathematischen Voraussetzungen erfüllt, um bei diesem Experiment auch Berechnungen durchführen zu können. Auch kann der Einfluss der Reibungskraft auf die ermittelte Beschleunigung berechnet werden. Zusätzlich können die SuS nun bestimmen, in welchem Winkel gegebene Massen zueinander stehen müssen, um ein Kräftegleichgewicht erzeugen zu können.
Merksätze für die Sekundarstufe II:
- Wirken mehrere Kräfte auf einen Körper, so addieren sich diese vektoriell zu einer wirkenden Nettokraft.
- Der Betrag, der aus zwei Kräften resultierenden Nettokraft lässt sich über den Kosinussatz bestimmen.
- Wird ein Körper durch zwei oder mehr Kräfte beschleunigt, so bewegt er sich in die gleiche Richtung wie die, in welche die Nettokraft wirkt.
Versuchsanleitung
Materialien
- 3 feste Rollen
- Stativmaterial für die 3 Rollen (in der Höhe verstellbar)
- 1 weißes Blatt Papier A2
- feine Glasperlen (für eine möglichst reibungsfreie Bewegung)
- 1 erhöhte ebene Oberfläche (in diesem Fall ein runder Tisch)
- 1 Puck mit einer Masse von mPuck =100g aus Stahl
- Massestücke 3 x (10g, 20g, 50g, 100g)
- Angelsehne oder Bindfaden
- HD Viedokamera für eine genauere Auswertung der Bewegung
Aufbau und Durchführung
Grundsätzlich lässt sich der Versuch in 2 Teile untergliedern. Im ersten Teil wird der statische Fall betrachtet, bei dem die wirkende Nettokraft gleich null ist. Dazu wird eine Kraft F1 konstant gehalten und die anderen Kräfte F2 und F3, bzw. die Winkel zwischen den Kräften können variiert werden.
Im 2. Teil wird dann die aus mehreren Kräften (welche sich nicht gegenseitig aufheben) resultierende Bewegung untersucht.
Zunächst wird das weiße Blatt Papier so ausgeschnitten, dass es deckungsgleich auf die erhöhte Oberfläche passt. Damit ist sichergestellt, dass man eine einheitliche Oberfläche mit einem (relativ) geringen Reibungskoeffizienten hat. Außerdem können auf dem Papier verschiedene Winkel eingezeichnet werden. Damit fällt die spätere Ausrichtung der angreifenden Massen leichter. Das Lineal, welches im Bild 1 zu sehen ist wird erst im 2. Teil gebraucht und muss im 1. Teil entfernt werden. Die festen Rollen werden an 3 Stativen fixiert und auf die Höhe der Experimentieroberfläche angepasst. Anschließend können für den symmetrischen Aufbau die Stative im Winkel von 120° zueinander um den Tisch angeordnet werden.
Der Puck wird nun in der Mitte vom Tisch platziert und die 3 Massen m1, m2 und m3 über die festen Rollen daran fixiert. Aufgrund der Gravitationskraft entstehen dadurch die Kräfte F1, F2 und F3, welche über die Fäden direkt auf den Puck wirken. Abschließend kann noch eine Feinjustierung stattfinden, damit die Winkel auch korrekt eingestellt sind. (Aufgrund der Haftreibung wird sich der Puck auch bei leicht abweichenden Winkeln nicht bewegen.)
Weitergeführt wird dieses Experiment mit nahezu demselben Aufbau. Es bietet die Möglichkeit die Addition der Kräfte bei unterschiedlichen Winkeln zwischen den Kraftvektoren zu betrachten. Dabei können die angreifenden Kräfte, oder die Winkeln modifiziert werden. So könnte man mit den Massen 30g, 40g und 50g ebenfalls ein Kräftegleichgewicht erzeugen, wobei die Winkel α = 37° und β = 53° (gerundete Werte) sein müssen (siehe Skizze ...). An dieser Stelle können SuS selbst experimentieren und versuchen Konstellationen zu finden, unter denen die Nettokraft gleich null ist.
Für die Durchführung des 2. Teils wird nun der Puck fixiert und die Masse m1 entfernt. Sobald die Fixierung gelöst ist, wird der Puck durch die anderen Massen m2 und m3 beschleunigt. Um die Bewegung des Pucks genauer untersuchen zu können wird nun zentral über dem Tisch eine HD Kamera angebracht, welche den Experimentiervorgang aufnimmt.
Beobachtungen
Versuchsteil 1
Ist der Versuch wie in der Durchführung beschrieben aufgebaut worden, so stellt man fest, dass der Puck, obwohl durch die Massen 3 Kräfte auf ihn wirken, nicht bewegt. Ändert man allerdings einen der Winkel oder eine Masse so wird der Puck beschleunigt. Dabei ist zu beobachten, dass die Beschleunigung nicht entlang der 3 Kräfte verläuft.
Mit anderen Massen lassen sich auch Gleichgewichte herstellen, wobei es für drei bestimmte Masse immer nur eine "richtige" Winkelverteilung gibt.
Versuchsteil 2
Im Zweiten Teil des Experimentes wurde der Puck fixiert und die Masse m1 entfernt. Nachdem die Fixierung an dem Puck entfernt wurde, kann man beobachten wie dieser beschleunigt wird. Dabei ist die Beschleunigungsrichtung nur dann exakt zwischen der Wirkungsrichtung von F2 und F3, wenn die beiden Massen gleich groß sind. Dieses Experiment wurde mehrfach durchgeführt. Dabei wurde die Bewegung des Pucks mit einer HD-Kamera aufgezeichnet und genauer untersucht.
Messwerte und Ergebnisse
Versuchsteil 1
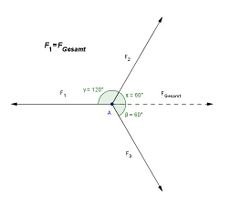
Aufgrund der Superposition von Kräften ergibt sich der Betrag und die Richtung resultierenden Kraft FGesamt aus den Kräften F1, F2 und F3 (siehe Skizze 3).
Aus der Beobachtung im ersten Versuchsteil lässt sich folgern, dass sich die Kräfte aufgrund ihrer Ausrichtung zu "null" addieren, sodass keine Nettokraft auf den Puck wirkt. Diese Beobachtung lässt sich wie folgt begründen:
In der Skizze 3 ist veranschaulicht, dass die Kräfte F1 und FGesamt exakt in entgegengesetzte Richtung wirken und die gleiche Länge haben. Damit gilt:
Folglich ist die wirkende Nettokraft gleich null.
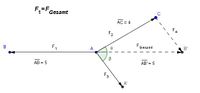
Eine weitere Konstellation aus Massen und Winkel, bei der die Nettokraft gleich null ist, ist in Skizze 4 dargestellt.
Versuchsteil 2
Am einfachsten lassen sich aufgezeichnete Bewegungen mithilfe von Videoanalyseprogrammen wie zum Beispiel Viana auswerten.
Alternativ kann man, wie in Bild 1 dargestellt, ein hinreichend genaues Maßband in die Kamera legen. Untersucht man nun jedes einzelne Bild der Aufnahme kann man bei einem konstanten Δt die zugehörigen Werte für Δs abmessen.
In beiden Fällen ist es dass Ziel die Beschleunigung zu ermitteln und damit einen Rückschluss auf die wirkende Kraft zu erhalten.
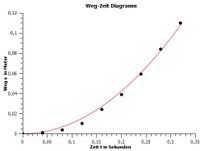
Sowohl das Experiment wurde 6 mal in der einfachen Variante und 6 mal unter Einsatz der Glasperlen durchgeführt. Damit konnte ein Mittelwert über die Messreihen ermittelt werden. Im Bild 3 sind die Messwerte für das Experiment eingetragen. Der rot eingezeichnete Graph ist ein Polynomfit 2. Grades. Aus der damit erhaltenden Parabelfunktion lässt sich durch 2-maliges Ableiten die Beschleunigung des Pucks ermitteln.
Diese Messreihe ergab für die Beschleunigung des Pucks rund 2,1 m/s², was einer wirkenden Kraft von ca. 0,63 N entspricht.
Rechnerisch erhält man allerdings einen theoretischen Wert von 1 N für die Nettokraft.
Ein Wichtiger Aspekt, der zu dieser Abweichung führt sind die auftretenden Reibungskräfte. Diese werden genauer im folgenden Abschnitt untersucht:
Weiterführendes Experiment
Aufbauend auf die Erkenntnisse des 2. Versuchsteil bietet sich dieses Experiment an, es genauer auf Fehler zu untersuchen. Dabei ist die Gleitreibung des Pucks der zentrale Punkt, welcher näher diskutiert werden muss. Dafür können am Startpunkt und entlang der geplanten Bewegungsrichtung des Pucks feine Glasperlen verstreut werden, welche die Gleitreibung erheblich verringern. Die Auswertung des Experiments erfolgt analog zu Versuchsteil 2.
Zusätzlich können hier Messwertfehler durch den Aufbau und die verwendeten Geräte thematisiert werden.
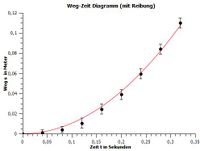
Man kann in beiden Diagrammen gut erkennen, dass alle Messwerte innerhalb der Fehlertolleranzen liegen. Die Messwertfehler setzen sich aus der dem Konfidenzintervall, welches den Beitrag der zufälligen Messabweichungen zur gesamten Messunsicherheit angibt und der Genauigkeit des Maßstabs zusammen. Das Konfidenzintervall lässt sich über folgende Formel berechnen: [6]
- , wobei insgesamt 6 Messreihen aufgenommen worden sind.
Damit gilt n = 6 und i= 1...6.
- , wobei insgesamt 6 Messreihen aufgenommen worden sind.
Der Gerätefehler des Maßstabs wurde auf 200 μm + 10-3 • L, wobei L die gemessene Länge angibt, abgeschätzt.
In der ersten Messreihe wurde eine Beschleunigung von rund 2,1 m/s², was einer wirkenden Kraft von ca. 0,63 N entspricht.
Ausgehend vom 2. newtonschen Axiom und unter Berücksichtigung der Gleitreibung würde man folgenden Wert erwarten:
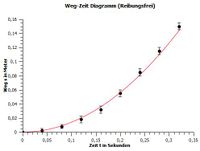
Die Auswertung des zweiten Diagramms (siehe Bild 5) ergab eine Beschleunigung von rund 2,8 m/s². Da in diesem Fall der Reibungswiderstand vernachlässigbar klein ist, müsste der Wert allerdings bei
- liegen.
In beiden Experimenten liegt der ermittelte Wert für die Beschleunigung deutlich zu niedrig, auch wenn im reibungsfreien Fall die Abweichung geringer ist. Der Fehler muss also systematisch in beiden Experimenten aufgetreten sein.
Ein wichtiger Punkt, der nicht berücksichtigt worden ist, sind festen Rollen an denen ebenfalls ein Reibungseffekt auftritt. Des Weiteren ändert sich mit der Bewegung auch der Winkel der angreifenden Kräfte, wodurch die resultierende Kraft immer kleiner wird. Da das Experiment aber nur über eine kurze Strecke beobachtet worden ist, ist dieser Fehler vergleichsweise klein.
Sicherheitshinweise
Benutzt man größere Massen von 50 - 100 g wird der Körper in der Mitte sehr stark beschleunigt. Das potentielle Verletzungsrisiko ist zwar gering, aber es kann passieren, dass der Körper vom Tisch fällt, oder Teile der Fixierung zerstört werden. Auch wird die Auswertung des Experimentes bei größeren Beschleunigungen immer ungenauer.
Bei den feinen Glasperlen sollte darauf geachtet werden, dass diese nicht in Kontakt mit Mund, Nase, Augen oder Ohren kommen.
Literatur
- [1] Physik, Lehr- und Übungshandbuch, Douglas C.Giancoli, 3. erweiterte Auflage 2010
- [2] Physik, Gymnasiale Oberstufe, Duden Paetec Schulbuchverlag, 1. Auflage 2003
- [3] Schülervorstellungen in der Physik, Aulis Verlag, Rainer Müller, Rita Wodzinski, Martin Hopf, 3. unveränderte AuflagePraxis-
- [4] Schülervorstellungen in der Physik, Rita Wodzinski: Untersuchungen von Lernprozessen beim Lernen Newtonscher Mechanik im Anfanghsunterricht. Münster: Lit-Verlag, 1996
- [5] Senat für Bildung Jugend und Sport, 2006: Rahmenlehrplan Physik, Sekundarstufe I und II, Oktoberdruck AG Berlin
- [6] Physikalisches Grundpraktikum - Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik, Humboldt-Universität zu Berlin, Institut für Physik, 2007












![{\displaystyle {\overline {s}}=\pm 1\cdot {\sqrt[{2}]{\frac {\Sigma (x_{i}-{\overline {x}})^{2}}{n\cdot (n-1)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d263efada242155acb5472386f4d9a1d16d7e1c)

