Über Wechselstromwiderstände zu einer Frequenzweiche

Über Wechselstromwiderstände zu einer Frequenzweiche
Platine der untersuchten Frequenzweiche
Kurzbeschreibung
Aufbau und Funktion einer einfachen Frequenzweiche verstehen, Frequenzabhängigkeit von Wechselstromwiderständen mit "Cassy" aufzeichnen.
Kategorien
Elektrizitätslehre
Einordnung in den Lehrplan
Geeignet für:	Sek. II
Basiskonzept:	System, Wechselwirkung, Energie
Sonstiges
Durchführungsform	Lehrerdemoexperiment, Schülergruppenexperiment, Schülerdemoexperiment
Anzahl Experimente in dieser Unterkategorie	3
Anspruch des Aufbaus	mittel
Informationen
Name:	Dirk Rathke
Kontakt:	${\text{rathkedi}}$@${\text{hu-berlin.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Tobias Ludwig

Dieses Experiment soll dazu beitragen, den Aufbau und die Funktion einer einfachen Frequenzweiche zu verstehen. Eine Frequenzweiche teilt einen breiten Frequenzbereich, im allgemeinen ein elektrisch kodiertes Signal, in einzelne schmale Frequenzbereiche auf. Man spricht deshalb auch von Frequenzfiltern. Diese Filterung wird durch eine Zusammenschaltung von Widerständen, Kondensatoren und/oder Spulen realisiert. Dabei spielt der frequenzabhängige Wechselstromwiderstand der Bauelemente Kondensator und Spule eine große Rolle. Eine Frequenzweiche wird zum Beispiel genutzt, um hohe bzw. tiefe Frequenzen eines elektrischen Musiksignals getrennt an sogenannte Hoch- und Tieftöner in Lautsprecherboxen weiterzuleiten.
Um zu verstehen, wie diese Bauelemente Frequenzen aufteilen bzw. filtern, soll dafür der frequenzabhängige Wechselstromwiderstand eines Kondensators und einer Spule untersucht werden. Aus diesen Erkenntnissen und dem Wissen über die Kirchhoffschen Regeln wird auf das frequenzabhängige Verhalten einer Zusammenschaltung der Bauelemente als Frequenzweiche geschlossen.
Dieses Experiment könnte als Angebot innerhalb des Wahlthemas Wechselstrom (nach Berliner RLP für Sek. II) genutzt werden. Interessanter jedoch ist die Einbindung der Frequenzweiche, als eine technische Anwendung von Wechselstromschaltungen, in einen lebenspraktischen Kontext. Für die Untersuchungen in den dargestellten Experimenten sind Kenntnisse über komplexe Größen nicht notwendig. Vorteilhaft sind aber Kenntnisse über die Konzepte zur Beschreibung von Strom und Spannung in Reihen- und Parallelschaltungen sowie des Wechselstromwiderstands von R (ohmscher Widerstand), L (Induktivität als Spule) und C (Kapazität als Kondensator).

Wichtig sind die folgenden Zusammenhänge für das Verstehen der Experimentieranleitung und für die Begriffsnormung. Der komplexe Wechselstromwiderstand ergibt sich nach Z = R + jX, dabei sind R der Realanteil (auch ohmscher Widerstand) und X der Imaginäranteil (frequenzabhängiger Blindwiderstand). Der frequenzabhängige Blindwiderstand X kann sich aus einem kapazitiven X_C oder induktiven X_L Blindwiderstand ergeben. Für die idealisierten Bauelemente ergibt sich demnach für einen Widerstand Z = R, für einen Kondensator Z = X_C = -j/ωC und für eine Spule Z = X_L = jωL (ohne j ist der Betrag des Widerstands gemeint) mit ω = 2πf. In realen Bauteilen treten die Widerstandskomponeneten gemischt auf. Der Wechselstromwiderstand kann messtechnisch z.B. ermittelt werden aus |Z| = U_eff/I_eff.

Didaktischer Teil

Die Frequenzweiche als sinnstiftender Kontext.
Gerade die „trockenen“ Modelle zur Beschreibung der Grundelemente der E-Technik (Widerstand, Spule und Kondensator) in Wechselstromschaltungen bereiten nicht nur Schülerinnen und Schülern große Schwierigkeiten. Dabei unterstützt die mathematische Beschreibung der E-Technik nicht unbedingt deren Verständnis und wird oft als Problem im Physikunterricht benannt. Häufig fehlt der lebensnahe Bezug, "um sich darunter etwas vorzustellen".
Ausgehend von diesen Voraussetzungen wird das Lehrer- oder Schülerexperiment traditionell als eine aktive Unterstützung der Wissenskonstruktion gesehen. Neben den Vorteilen, wie z.B. der intersubjektiven Prozesse beim Experimentieren, weist Börlin auch auf Begrenzungen hin. Das Experiment in der Schule muß nicht unbedingt zum Verständnis von physikalischen Inhalten beitragen. Denn oft kann die naturwissenschaftliche Erklärung der gezeigten Phänomene nicht mit Alltagserfahrungen verknüpft werden und wird somit als fremd empfunden. Dieses Gefühl der Fremdheit wirkt sich nicht positiv auf die kognitiven Prozesse beim Lernen aus.
Deshalb versucht Muckenfuß eine Erweiterung der historisch gewachsenen Struktur des Physikunterrichts nach Wagenstein . Er schlägt eine Ausgestaltung des Physikunterrichts mit lebenspraktisch bedeutsamen Themen vor, die in sogenannte Rahmenkontexte (z.B. Sehen und Erkennen - Optik) eingebunden sind. „Die Rahmenkontexte liefern die sinnstiftenden Zusammenhänge, in denen die Sachstrukturen erarbeitet werden. Zugleich bilden sie Brücken zur Lebenspraxis oder zu anderen Unterrichtsfächern.“^[2] Der kontextbezogene Unterricht bildet einen Gegenpol zum fachsystematischen und das Experiment dient nicht nur als Einstieg oder Ausblick. Der Kontext entscheidet über die physikalische Sachstruktur und die physikalischen Fachinhalte dienen seiner Erschließung.
Die Einbettung einer Sachstruktur innerhalb eines Kontextes nach Muckenfuß soll kurz mit den hier beschriebenen Experimenten dargestellt werden. Zum besseren Verständnis können auch seine zahlreichen Beispiele in "Lernen im sinnstiftenden Unterricht"^[2] betrachtet werden. Die hier beschriebenen Experimente könnten so z.B. innerhalb des Rahmenkontextes „Information und Kommunikation“^[2] mit dem Teilkontext elektrisches Signal genutzt werden. Als kontextbezogener Inhalt bieten sich der Frequenzfilter als eine Wechselstromschaltung an und als struktureller Inhalt die Frequenzabhängigkeit der Wechselstromwiderstände von L und C im Wechselstromkreis (X_L = ωL und X_C = 1/ωC). Das Anwendungsbeispiel eines Frequenzfilters (Schaltung aus Wechselstromwiderständen) wäre die konkret vorliegende Frequenzweiche. Aus dieser Struktur kann eine Unterrichtseinheit abgeleitet werden.
Im Berliner Rahmenlehrplan ist das Konzept der Kontextualisierung mit den Hinweisen darauf aufgenommen: dass ein Themenfeld in einem größeren Kontext erfasst wird, ein kontextbezogenes Lernen bezüglich der Basiskonzepte erfolgt und naturwissenschaftliche Kenntnisse auf neue bzw. komplexe Fragestellungen übertragen werden .

Versuchsanleitung

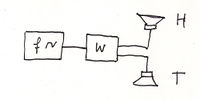
Für das Verstehen einer Frequenzweiche, hier aufgebaut mit Spule und Kondensator, sind drei Experimente dokumentiert. Das erste Experiment zeigt die Frequenzabhängigkeit des Wechselstromwiderstandes eines Kondensators im Wechselstromkreis, das zweite die Frequenzabhängigkeit des Wechselstromwiderstandes einer Spule. Mit CassyLab werden automatisch Kennlinien der Abhängigkeit des Wechselstromwiderstandes (auch Impedanz genannt) von der Frequenz aufgezeichnet. Dazu empfiehlt sich die Nutzung der mit der Software bereitgestellten Grundeinstellung für R-L-C-Messungen im Wechselstromkreis, siehe dazu CASSY® Lab -Handbuch der LEYBOLD DIDACTIC GmbH. Am Ende, im dritten Experiment, werden Kondensatur und Spule in Zusammenschaltung als Frequenzweiche, qualitativ mittels "Tonsignal", aus einem Frequenzgenerator untersucht. Dabei wird mit zwei Lautsprechern die akustische Ausgabe der getrennten Frequenzbereiche auditiv überprüft.

Für die Experimente werden folgende Geräte und Zubehör benötigt:

• Kondensator 1µF, Spule 25 H (12 Ohm),
• Frequenzweiche "Visaton HW 2/70 NG (2 Weg) 8 Ω" (siehe Versuch 3) oder vergleichbare Modelle, Bezug über Elektronikhandel
• Computer mit Schnittstelle und Software CassyLab
• USB-Kabel (o.a. entsprechend der Schnittstelle)
• Power-Cassy mit Netzteil
• Sensor-Cassy mit Netzteil
• Frequenzgenerator (Sinus bis 10 kHz)
• 2 Lautsprecher (wenn möglich Hoch- bzw. Tieftöner, i.d.R. 4 - 8 Ohm)
• Steckbrett, Verbinder/Leitungen (6 Stück),
• Netzstecker

Versuch 1 - Frequenzabhängigkeit des Wechselstromwiderstandes eines Kondensators

Im ersten Versuch soll die Frequenzabhängigkeit des Wechselstromwiderstandes eines Kondensators untersucht werden.

Aufbau

Bild 1: Schematisches Schaltbild

Bild 2: Foto Schaltungsaufbau

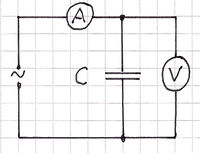
Der Signalausgang des Power-Cassy wird als Spannungsquelle geschaltet und die Spannungs- (U_B1) und Stromeingänge (I ₂) des Sensor-Cassy als Spannugs- und Strommesser. Das Sensor-Cassy wird mit dem Power-Cassy über eine gemeinsame Schnittstelle zusammengesteckt, beide erhalten jeweils eine externe Stromversorgung. Der Computer wird über eine entsprechende Schnittstelle (z.B. USB) an das Sensor-Cassy angeschlossen. Der Schaltungsaufbau kann dem schematischen Schaltbild in Bild 1 entnommen werden. Das Bild 2 zeigt den kompletten Aufbau.

Durchführung

Im Startmenü von Cassy-Lab sollten über die Auswahl "Beispielexperimente" die Grundeinstellungen vom Experiment "R-L-C-Messungen im Wechselstromkreis" geladen werden. Damit werden die Messeingänge U_B1 und I₂ von Cassy-Lab automatisch belegt (ggf. Schaltungsaufbau korrigieren), wie auch der Spannungsausgang mit automatischen Frequenzlauf. Ebenso werden die Messbereiche festgelegt und die Messwertauswertung mit Diagrammen geladen. Die eingestellten Parameter und die Messoberfläche können einfach modifiziert werden. Überflüssige Diagramme und Anzeigen sollten geschlossen werden, bis eine Programmoberfläche wie im Bild 3 erreicht ist. Natürlich besteht die Möglichkeit, alle notwendigen Einstellungen neu einzugeben und Diagramme anzulegen, was relativ aufwendig ist. 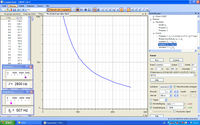Der Messbereich für die Frequenz ist auf f₀ = 0,5 bis 3 kHz = Stoppbedingung (siehe Bild 3) einzustellen. Der Wechselstromwiderstand bzw. die Impedanz Z_C wird automatisch ermittelt nach Z_C = U_B1/I₂ aus den gemessenen Größen Spannung U_B1 und Strom I₂. Das Diagramm zum Aufzeichnen des Graphen Z_C = Funktion (f) ist konfiguriert
Nun kann der Messvorgang in Cassy-Lab gestartet werden. Da die Messpunkte langsam angefahren werden und die Kurve langsam durchlaufen wird, sollte am Anfang etwa 10 s gewartet werden, bis die ersten Aufzeichnungen im Diagramm sichtbar werden. Eine Probemessung wird empfohlen.

Ergebnisse und Diskussion

Bild 3: Kennlinie Kondensator

Bild 3.a: linearisierte Kennlinie Kondensator

In CassyLab wird der funktionale Zusammenhang zwischen dem kapazitiven Wechselstromwiderstand Z_C und der Frequenz f als Graph dargestellt, Bild 3. Dabei wird von einem idealen Kondensator ausgegangen. Ohmsche und induktive Anteile werden vernachlässigt, da diese vergleichbar klein sind und hier auch eine qualitative Aussage genügt. Dem Graphen kann entnommen werden, dass mit Zunahme der Frequenz der Wechselstromwiderstand des Kondensators kleiner wird. Diese "grobe" Erkenntnis wird später für die Erklärung der Funktion der Frequenzweiche benötigt.
Als eine Erweiterung der Auswertung kann der Kurventyp einer umgekehrt proportionalen Funktion zugeordnet werden. Dazu werden die Messwerte (links in Bild 3 angezeigt) in einer grafische Darstellung ausgewertet als der Zusammenhang zwischen dem Wechselstromwiderstand Z_C des Kondensators und dem Reziproken der Frequenz 1/f. Das Bild 3.a zeigt einen annähernd linearen Verlauf.

Versuch 2 - Frequenzabhängigkeit des Wechselstromwiderstandes einer Spule

Im zweiten Versuch soll die Frequenzabhängigkeit des Wechselstromwiderstandes eine Spule untersucht werden.

Aufbau

Der Schaltungsaufbau kann vom Kondensatorversuch (s.o.) übernommen werden. Der Kondensator ist durch die Spule zu ersetzen.

Durchführung

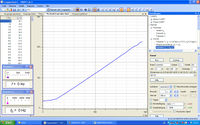
Die Einstellungen in Cassy-Lab können vom Kondensatorversuch mit leichter Konfiguration übernommen werden. Der Messbereich für die Frequenz ist auf f₀ = 0 bis 1 kHz (siehe Bild 4) und die Z_L-Achse von 0 - 300 Ω einzustellen. Der Wechselstromwiderstand bzw. die Impedanz Z_L ergibt sich auch hier aus der Spannung U_B1 und dem Strom I₂ nach Z_L = U_B1/I₂. Der Messvorgang kann nun in Cassy-Lab gestartet werden und wieder sind etwa 10 s abzuwarten, da die Messpunkte langsam angefahren werden.

Ergebnisse und Diskussion

Bild 4: Kennlinie Spule

In CassyLab wird der funktionale Zusammenhang zwischen dem Wechselstromwiderstand Z_L und der Frequenz f als Graph dargestellt, siehe Bild 4. Dabei wird hier von einer idealen Spule ausgegangen. Ohmsche und kapazitive Anteile werden vernachlässigt, da hier eine qualitative Aussage genügt. Der Kurventyp kann im wesentlichen durch den konstanten Anstieg (außer am Anfang) einer linearen Funktion zugeordnet werden. Das bedeutet es besteht ein proportionaler Zusammenhang zwischen demWechselstromwiderstand Z_L und der Frequenz f. Das heißt, mit Zunahme der Frequenz steigt proportional der Wechselstromwiderstand der Spule. Diese Erkenntnis wird später für die Erklärung der Funktion der Frequenzweiche benötigt. Der Schnittpunkt mit der Z-Achse gibt den Ohmschen Widerstand an und bei geringer Frequenz ist kaum eine Zunahme des Wechselstromwiderstands sichtbar (flacher Anstieg). Hier liegt ein reales Bauteil mit Z = R + jX_L vor. Der "Wackler" am Ende des Graphen zeigt eine Messunsicherheit, mehr dazu in der Zwischenauswertung.

Fazit mit didaktischer Diskussion zu Versuch 1 und 2

Durch das unmittelbare Anzeigen der Messkurven in Cassy-Lab können die Schülerinnen und Schüler leicht den Zusammenhang zwischen der Frequenz und der Wechselstromwiderstände von Kondensator und Spule aus den Graphen ablesen. Dadurch entfällt das meist aufwendige Aufnehmen von Messwerten und das eigene grafische Darstellen der Messwerte, damit kann Zeit und Aufmerksamkeit auf die Kontextualisierung verwendet werden. (Es ist aber möglich die Messwerte aus Cassy-Lab auszulesen.) Ein Nachteil von Cassy-Lab ist, dass die Messpunkte langsam angefahren werden. Und es werden einzelne (diskrete) Messpunkte aufgenommen, die als durchgängige Kurve dargestellet werden. Diese Darstellung entspricht keiner exakten physikalischen Darstellung und sollte thematisiert werden. Der Messfehler von den Cassy-Geräten wird mit 1% vom Bereichsendwert angegeben, die Fehler der Bauelemente Kondensator und Spule sind vergleichsweise größer mit bis zu 10% (Herstellerangabe). Aber da es im Experiment nur um die typischen Kennlinien geht, können die Fehler diskutiert, müssen aber nicht besonders berücksichtigt werden. Eine besondere Fehlerquelle, wie schon erwähnt, kann sich durch das "Einschwingen" der Eingangsfrequenz ergeben, wenn die Zeit zum Anfahren der Messpunkte zu kurz gewählt wird (siehe Ende der Messkurve von der Spule, es kann sich auch ein zackiger Verlauf in der Messkurve ergeben). Weiterhin sollte die technische Grenze des Schaltungsaufbaus bezüglich der Effekte hoher Frequenzen (z.B. Skineffekt) berücksichtigt werden. Deshalb wurde hier nur bis 3 kHz gemessen.

Versuch 3 - Zusammenschaltung von C und L als Frequenzweiche

Im dritten Versuch soll die Funktion einer Frequenzweiche, d.h. die Frequenzabhängigkeit einer Zusammenschaltung von Kondensator und Spule, untersucht werden. Zum besseren Verständnis sollen hier Frequenzen nacheinander über einen Frequenzgenerator durchlaufen werden, dabei werden tiefe und hohe Frequenzen von der Weiche gefiltert. Die Trennung von tiefen und hohen Frequenzen wird rein akustisch über Lautsprecher (Hoch- und Tieftöner) wahrgenommen. Auf Grundlage der Erkenntnisse aus den vorhergehenden Experimenten und der aktuellen Beobachtung sollen Erklärungsversuche über die Funktion einer Frequenzweiche bzw. Frequenzfilter unternommen werden.
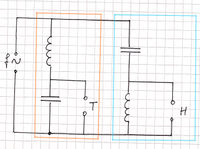
Für Frequenzweichen und -filter finden sich verschiedene Schaltungen in der Literatur. Hier wird nur die eine Schaltung nach Bild 5 untersucht, weil die Schaltung aus einer einfachen Reihen- und Paralleschaltung von Kondensator und Spule aufgebaut ist.

Aufbau

Bild 5: Schematisches Schaltbild Frequenzweiche

Bild 6: Platine der Frequenzweiche

Bild 7: Versuchssaufbau Frequenzweiche schematisch

Hier kommt die handelsübliche Frequenzweiche (Visaton Frequenzweiche HW 2/70 NG, 2 Weg, 8 Ω) zum Einsatz, weil auf dieser sehr gut sichtbar nur Spulen und Kondensatoren jeweils in Reihe geschaltet sind. Diese bilden die beiden parallel geschalteten Frequenzfilter. Der im Bild 5 orange umrandete Filter überträgt die tiefen und der blau umrandete Filter die hohen Frequenzen. Auf der Platine sind die Anschlußpins für den Tieftöner mit "B" und für den Hochtöner mit "H" bezeichnet. Dort werden die Lautsprecher angeschlossen. Am Weicheneingang, mit "IN" auf der Platine bezeichnet, wird der Frequenzgenerator angeschlossen, siehe Bilder 6 und 7. Für einfache Steckverbindungen sollten kurze Leitungen mit Stecker an den Lötpins angelötet werden. Damit sind die Lautsprecher (Impedanz nach Herstellerangabe, hier 8 Ohm) jeweils über eine Spule bzw. einen Kondensator angeschlossen, vergleiche Bild 5. Die beiden Lautsprecher (T und H) sollten mit ca. 2 m Abstand voneinander vor den Zuhörern stehen und der Schallkegel auf die Zuhörer ausgerichtet sein, siehe Bild 7.
Folgende Spulen und Kondensatoren sind auf der Platine montiert (vergleiche Bild 6):

Bauelemente:	Tief	Hoch
Spule:	0,1 mH	0,3 mH
Kondensator:	10 µF	3,3 µF

Die Übernahmefrequenz (siehe Herstellerangabe), d.h. die Trennung zwischen den tiefen und hohen Frequenzen, wird vom Hersteller mit 3 kHz angegeben.

Durchführung

Der Frequenzbereich des Frequenzgenerators wird von 0 bis 10 kHz durchlaufen. Dabei werden tiefe, mittlere und hohe Töne aus den Lautsprechern hörbar. Der Durchlauf sollte in beide Richtungen wiederholt werden, damit sich die Wahrnehmung der Beobachter/Zuhörer auf den Tonwechsel einstellen kann.

Ergebnisse

Wenn am Eingang der Frequenzweiche ein Tonsignal mit niedriger Frequenz anliegt, werden deutlich tiefe Töne nur aus dem einen Lautsprecher (T) wahrgenommen. In der Nähe der Übernahmefrequenz von ca. 3 kHz hört man einen mittleren Ton aus beiden Lautsprechern (T und H). Bei weiterer Erhöhung der Frequenz findet ein Wechsel in der Lautstärke vom ersten zum zweiten Lautsprecher statt und im weiteren Verlauf sind die hohen Töne nur aus dem zweiten Lautsprecher (H) zu hören.

Auswertung

Aus den drei Experimenten soll die Funktion einer Frequenzweiche erklärt werden. Dazu wurde zuerst der frequenzabhängige Wechselstromwiderstand von Kondensator und Spule und anschließend die frequenzabhängige Übertragung/Filterung des elektrischen Tonsignals der Frequenzweiche untersucht. Auf eine reine mathematische Beschreibung der Schaltung der Frequenzweiche mittels komplexer Größen soll dabei verzichtet werden. Deshalb wird hier eine qualitative / halbquantitative Erklärung angeboten. Dazu wird die Frequenzabhängigkeit der Wechselstromwiderstände, wie in den Experimenten 1 und 2 ermittelt, tabellarisch zusammengefasst (vergleiche mit Kennlinien in Bild 3 und 4):

Wechselstromwiderstand	tiefe Frequenz	hohe Frequenz
Kondensator ZC	gross	klein
Spule ZL	klein	gross

Für die letzten Schritte werden die Kirchhoffschen Regeln benötigt. Jeder Filter (orange und blau im Bild 5) in der Frequenzweiche ist eine Reihenschaltung in der sich die Gesamtspannung (Eingangsspannung U_E) auf die Teilspannungen an den Bauelementen nach U_E = U_L + U_C aufteilt. Der Gesamtstrom der Frequenzweiche teilt sich auf die parallelgeschalteten Filter H und T auf und durchfließt jeweils Spule und Kondensator gleichermaßen. I = I_H + I_T. Auf den Zusammenhang |Z| = U_eff/I_eff wurde bereits eingegangen.
Das heißt, für den Filter T (Tiefton) in Bild 5 orange umrandet: bei tiefer Frequenz ist der Wechselstromwiderstand des Kondensators sehr groß und damit ist auch der Spannungsabfall über dem Kondensator groß, hingegen ist der Wechselstromwiderstand der Spule klein und somit der Spannungsabfall darüber klein. Bei Abnahme der Frequenz nähert sich die Ausgangsspannung |U_A| (Spannung über den Kondensator) der Eingangsspannung |U_E| an. Bei Zunahme der Frequenz verändern sich die Wechselstromwiderstände, die Spannungsabfälle darüber sind gegenläufig und die Ausgangsspannung nimmt ab. Der Höhe der Spannung (Betrag der Größe) entspricht die Lautstärke des hörbaren akustischen Signals. Deshalb sind aus dem Lautsprecher T (Tieftöner) die tiefen Töne lauter zu hören, als die hohen Töne. Ein Filter der praktisch nur tiefe Frequenzen überträgt, wird Tiefpassfilter genannt. Das Übertragungsverhältnis ergibt |U_A|/|U_E| → 1 für ω = 0 bzw. |U_A|/|U_E| → 0 für ω = ∞.
Für den Filter H (Hochton), in Bild 5 blaue umrandet, sind Spule und Kondensator vertauscht, dementsprechend verhält sich die Schaltung zur Frequenz umgekehrt. Das heißt die Ausgangsspannung ist bei tiefer Frequenz niedrig und nähert sich bei hoher Frequenz der Eingangsspannung an. Somit sind aus dem Lautsprecher H (Hochtöner) die hohen Töne lauter zu hören, als die tiefen Töne. Dieser Filter, der hohe Frequenzen durchlässt, wird Hochpassfilter genannt mit |U_A|/|U_E| → 0 für ω = 0 bzw. |U_A|/|U_E| → 1 für ω → ∞.
Im mittleren Frequenzbereich um 3 kHz besteht über Kondensator und Spule ein mittlerer Spannungsabfall, deshalb ist ein mittlerer Ton aus beiden Lautsprechern zu hören. (Hier kann die sogenannte Übernahmefrequenz gefunden werden.)
Fehlerbetrachtung und Ausblick: Da es sich beim dritten Experiment mehr um ein qualitatives Experiment handelt, kann auf eine Fehlerrechnung verzichtet werden. Aber wichtig ist der Hinweis auf eine Grenze des Versuchsaufbaus bezüglich hoher Frequenzen, da einfache Steckverbindungen und Leitungen benutzt werden. Im Zusammenhang damit kann auf technische Besonderheiten in der Hochfrequenztechnik eingegangen werden. Und zusätzlich bietet es sich an, die menschliche Sinneswahrnehmung als "Messinstrument" in Bezug auf ihre Möglichkeiten und Grenzen zu thematisieren.

Sicherheitshinweise

Es sollten die üblichen Sicherheitshinweise zum Arbeiten mit elektrischen Strom und Geräten mit Netzspannung, sowie mögliche Entladeströme von Kondensatoren beachtet werden.

Siehe auch

Informationen zu Cassy und Handbuch: http://www.ld-didactic.de/service/softwaredownload/cassy-s.html
Demtröder, Wolfgang: Experimentalphysik 2, Springer, 2009